Loi de Fresnel
Extension au cas des interfaces multiples.
On considère pour les calculs suivants les permittivités diélectriques et non les indices de réfraction
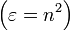
On peut définir des coefficients de Fresnel globaux pour un système constitué de plusieurs couches de milieux d'indices différents.
afin d'alléger les notations.
Cas de deux interfaces
Considérons 3 milieux
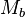
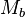
et
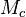
de permittivités diélectriques consécutives différentes, séparés par 2 interfaces planes.
Soit
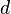
l'épaisseur de
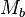
sont semi-
(
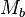
et
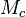
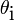
et
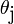
respectivement les angles d'incidence et de réfraction à l'interface entre
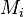
et
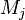
(avec i, j = a, b ou b, c).
Soit
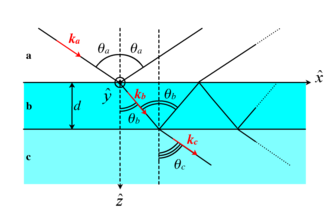
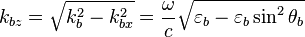
la composante suivant z du vecteur d'onde dans
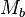
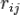
Soit
le coefficient de réflexion entre
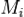
et
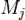
tel que défini précédemment
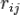
ou TE, ainsi que des angles
dépend de la polarisation TM
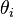
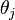
et
avec i, j = a, b ou b, c).
Les coefficients de transmission et de réflexion s'écrivent alors :
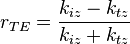
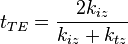
Discussion : les indices de réfraction étant complexes, la polarisation de l'onde transmise et réfléchie peut être modifiée par
rapport à l'onde incidente. Même dans le cas où ces indices seraient réels, dans le cas
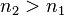
réflexion devienne négatif, l'onde réfléchie est alors déphasée de 180° par rapport à l'onde incidente.
La seule façon d'annuler le coefficient de réflexion est, en tenant compte des lois de Snell-
Par conséquent, une onde polarisée transverse électrique subit une réflexion dès qu'elle passe dans un milieu d'indice optique différent, ce qui n'est pas le cas d'une onde transverse magnétique (existence d'un angle de Brewster).
il se peut que le coefficient de
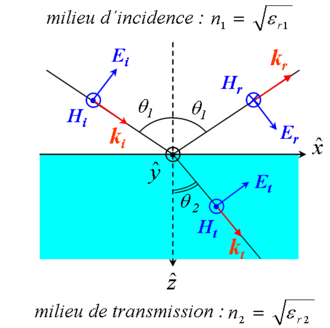
Cas des ondes transverses magnétiques
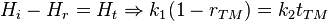
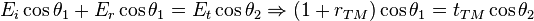
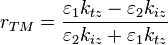
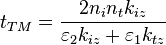
En introduisant, pour chaque milieu, la relation de dispersion
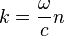
coefficients de Fresnel en fonction des caractéristique de l'incidence
on obtient les
(n1, θ1) et de la réfraction (n2, θ2) :
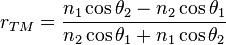
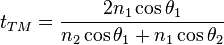
Remarque : suivant les ouvrages, les signes des coefficients de Fresnel diffèrent. Ceci provient des orientations arbitraires faites au départ. Par exemple, orienter sur la figure Hr vers l’avant, revient à remplacer, pour le calcul de r, Er par -
Discussion : le cas TM est remarquable à deux titres :
le coefficient de réflexion peut devenir nul pour un angle d'incidence, dit angle de Brewster ;dans certaines situations (interface métal-
Soient