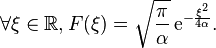Intégrale de Gauss
En mathématiques, une intégrale de Gauss est l'intégrale d'une fonction gaussienne sur l'ensemble des réels
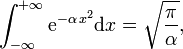
Sa valeur est reliée à la constante π par la formule
où α est un paramètre réel strictement positif. Elle intervient dans la définition de la loi de probabilité appelée loi gaussienne, ou loi normale.
Cette formule peut être obtenue grâce à une intégrale double et un changement de variable polaire.
Sa première démonstration connue est donnée par Pierre-
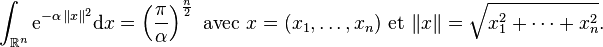
Si l'on travaille à n dimensions, la formule se généralise sous la forme suivante :
Agrandir Cliquez sur la photographie
Intégrabilité de la fonction
Comme l'intégrande est pair, il suffit, pour montrer qu'il est intégrable sur R, de prouver qu'il est intégrable sur R+. Cela résulte de ce qu'il est positif, continu, et négligeable à l'infini devant, par exemple, la fonction x -
Ainsi on a par exemple, avec les notations classiques :
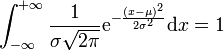
L'intégrande de l'intégrale de Gauss n'admet aucune primitive s'exprimant à l'aide des fonctions usuelles (exponentielle, etc.). Ceci oblige pour calculer cette intégrale à recourir à des méthodes plus ou moins « détournées », dont la plus classique et directe est celle qui utilise des intégrales doubles ; d'autres méthodes classiques existent dont une élémentaire, mais nettement plus longue, qui fait appel aux intégrales de Wallis et une autre qui utilise une fonction définie par une intégrale.
Cas particulier α = 1
La méthode classique de calcul utilise une intégrale double qu'on exprime en coordonnées cartésiennes, puis en coordonnées polaires.
Cas général α > 0
En effectuant dans l'intégrale de Gauss le changement de variable défini par , on obtient :
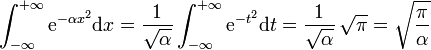
Calcul de l'intégrale de Gauss
Démonstration
Quelle que soit la technique utilisée, on a bien démontré que
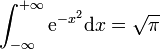
L'intégrale de Gauss comme valeur particulière de la fonction
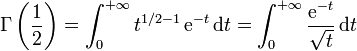
Le réel :
Transformée de Fourier d'une fonction gaussienne
Soit la fonction gaussienne :
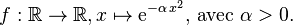
Elle est intégrable sur R. Sa transformée de Fourier
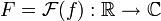
définie par
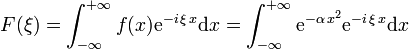
est telle que