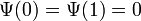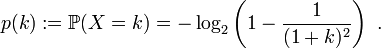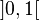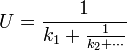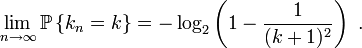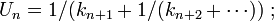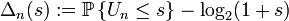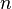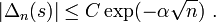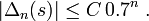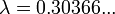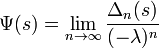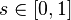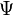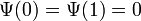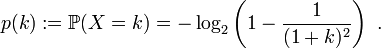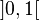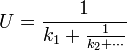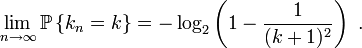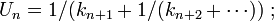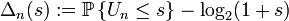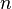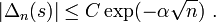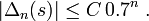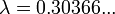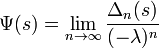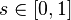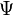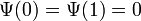En théorie des probabilités, la loi de Gauss-Kuzmin est une loi de probabilité discrète à support infini qui apparaît comme loi de probabilité asymptotique des coefficients dans le développement en fraction continue d'une variable aléatoire uniforme sur 0,1
Le nom provient de Carl Friedrich Gauss qui considéra cette loi en 1800, et de Rodion Kuzmin (en) qui donna une borne pour la vitesse de convergence en 1929
l'intermédiaire de la fonction de masse :
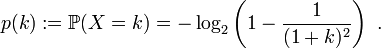
Soit une variable aléatoire uniforme sur U une variable aléatoire uniforme sur
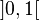
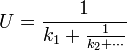
son développement en fraction continue.
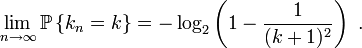
Ou de manière équivalente, en notant
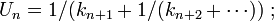
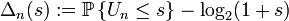
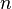
En 1928, Kuzmin donne la borne
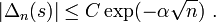
En 1929, Paul Lévy l'améliore en majorant
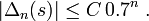
Plus tard, Eduard Wirsing montre que pour
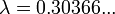
(la constante de Gauss-Kuzmin-Wirsing), la limite
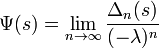
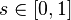
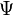
est analytique et satisfait