Quelle est la méthodologie de l'analyse sémiotique peircienne ?

La méthodologie découle des propriétés algébriques du treillis des classes de signes . Elle se déroulera en trois temps :1. analyse en classes de signes élémentaires.2. construction du "feuilletage" induit par les relations entre les classes.3. recherche d'un signe globalisant.

Pour en savoir plus:

Nous illustrons cette méthodologie avec un exemple tiré de l'Algèbre des signes (Marty, 1990) relative à l'étude du poème "Mathématiques" de Jules Supervielle.

(1)Quarante enfants dans une salle
Un tableau noir et son triangle(1)
(2)Un grand cercle hésitant et sourd
Son centre bat comme un tambour. (2)

(3)Des lettres sans mots ni patrie
Dans une attente endolorie.(3)

(4)Le parapet dur d'un trapèze(4)
(5)Une voix s'élève et s'apaise (5)
(6)Et le problème furieux
Se tortille et se mord la queue.(6)

(7)La mâchoire d'un angle s'ouvre
Est-ce une chienne ? Est-ce une louve ?(7)

(8)Et tous les chiffres de la terre
Tous ces insectes qui défont
Et qui refont leur fourmilière (8)
(9)Sous les yeux fixes des garçons.(9)

Le texte ext découpé en signes (les vers compris entre des chiffres identiques). Nous attribuons à chaque signe un objet (relativement consensuel nous semble-t-il) mais toujours discutable. Cependant les désaccords éventuels ne sauraient affecter la méthode qui se rapporte à la combinatoire des significations accordées aux signes découpés ci-dessus. Ce sont :

(1) classe "archétypique".
((2)cercle "animé".
(3)lettres "humanisées".
(4)parapet trapézoïdal.
(5)voix indéterminée.
(6)problème "animalisé".
(7)angle "animalisé";
(8)chiffres "insectisés".
enfants pétrifiés.

L'exercice appelle de toute évidence un grand renfort de néologismes et de guillemets, la langue offrant rarement les termes adéquats pour synthétiser la pensée d'un poète (c'est même un constat inhérent à l'expression poétique).

Aprés avoir étudié et arrêté la nature du signe proprement dit (en tant que mots de la langue ce sont tous des légisignes), puis la relation du signe à son objet et enfin sa relation à son interprétant, on l'affecte à l'une des classes du treillis. On obtient le sous-treillis suivant :

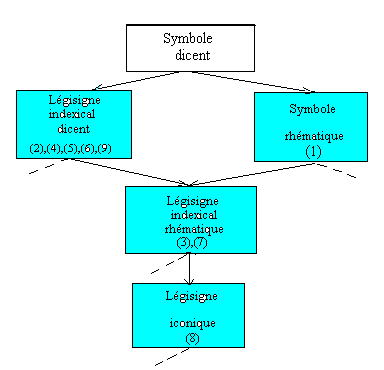
Les signes de (1) à (9) sont répartis dans les classes colorées en bleu. On constate que le signe global, c'est-à-dire l'objet de l'ensemble du poème, est nécessairement un symbole dicent, car cette classe de signes est la première, dans l'ordre du treillis, à contenir tous les signes partiels répertoriés ci-dessus. Ce signe "somme" est donc sémiotiquement équivalent à une proposition qui pourrait être "La mathématique est un animal monstrueux". Alors le "feuilletage" des signes montre (et à ce titre il est une icône-diagramme) la structure phénoménologique du plongement de la mathématique dans le règne animal réalisée dans ce poème. C'est une manière poétique de créer une tératologie.

Retour à l'index de la zone rouge. Parcours conseillé