Loi de Fresnel

Cas des ondes transverses électriques

Champ électrique polarisé perpendiculairement au plan d'incidence   

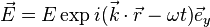
Considérons une onde plane électromagnétique :

où E représente l'amplitude complexe.

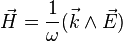
Dans le cas où le champ électrique incident est polarisé perpendiculairement au plan d'incidence, les composantes tangentielles du champ électrique et du champ magnétique sont continues :

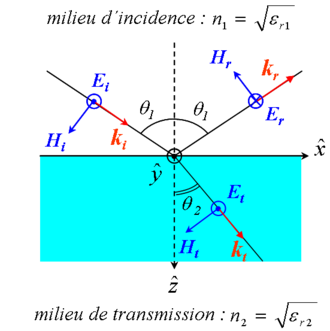
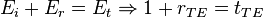
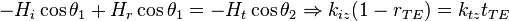
Les coefficients de transmission et de réflexion s'écrivent alors :

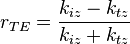
En introduisant, pour chaque milieu, la relation de dispersion

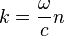
de Fresnel en fonction des caractéristiques de l'incidence

(n1, θ1) et de la réfraction (n2, θ2) :

on obtient les coefficients

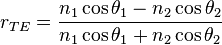
Discussion : les indices de réfraction étant complexes, la polarisation de l'onde transmise et réfléchie peut être modifiée par rapport à l'onde incidente.

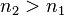
Même dans le cas où ces indices seraient réels, dans le cas

il se peut que le coefficient de réflexion devienne négatif, l'onde réfléchie est alors déphasée de 180°

par rapport à l'onde incidente.

La seule façon d'annuler le coefficient de réflexion est, en tenant compte des lois de Snell-Descartes, d'avoir

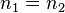
Par conséquent, une onde polarisée transverse électrique subit une réflexion dès qu'elle passe dans un milieu d'indice optique différent, ce qui n'est pas le cas d'une onde transverse magnétique (existence d'un angle de Brewster).

Cas des ondes transverses magnétiques

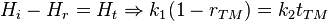
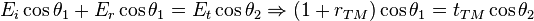
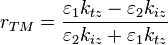
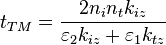
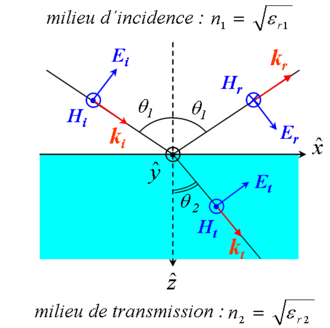
Remarque : suivant les ouvrages, les signes des coefficients de Fresnel diffèrent. Ceci provient des orientations arbitraires faites au départ. Par exemple, orienter sur la figure Hr vers l’avant, revient à remplacer, pour le calcul de r, Er par -Er ce qui changera le signe du coefficient.

Dans le calcul de filtres interférentiels, on tiendra compte des coefficients de Fresnel pour calculer le déphasage à la réflexion entre les couches du filtre.

Discussion : le cas TM est remarquable à deux titres :

e coefficient de réflexion peut devenir nul pour un angle d'incidence, dit angle de Brewster ;

dans certaines situations (interface métal-air), le dénominateur du coefficient de réflexion TM peut devenir nul (le coefficient devient infini). On obtient alors une onde réfléchie et une onde transmise sans onde incidente : l'étude du dénominateur précise alors les conditions de réalisation, les composantes des vecteurs d'ondes sont alors imaginaires.

Le processus emploie donc les ondes évanescentes, et provoque l'apparition des plasmons de surface.