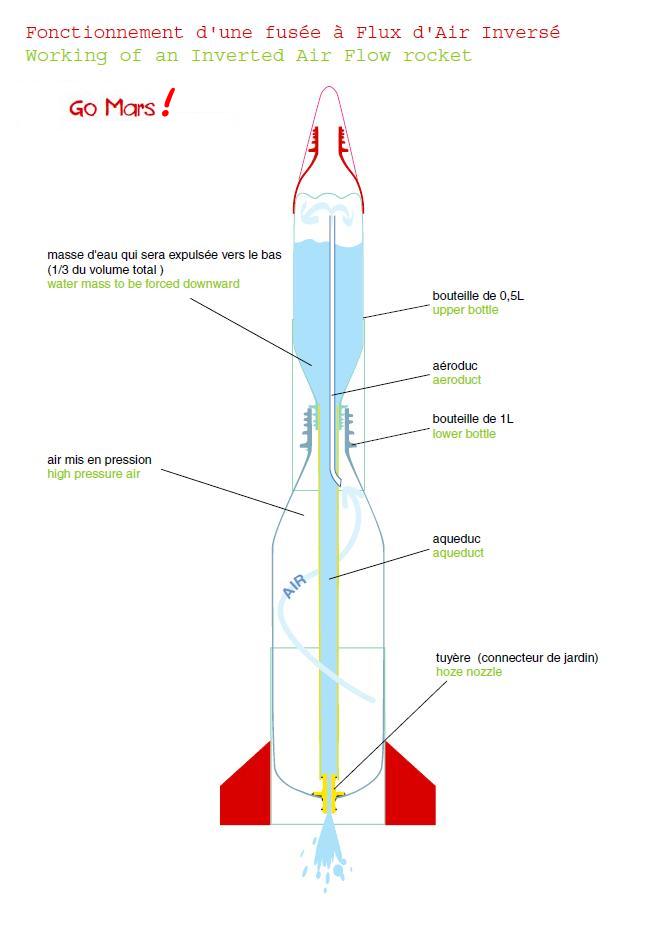
FONCTIONNEMENT D’UNE FUSÉE À EAU ... À FLUX D’AIR INVERSÉ

 (Working of an Inverted Air Flow water rocket)

Le schéma ci-dessous expose le fonctionnement d’une fusée à flux d’air inversé :

(cliquer sur l'image pour obtenir le même schéma en vectoriel .pdf que vous pourrez agrandir à volonté)

Pendant le fonctionnement du moteur, l’eau contenue dans la bouteille supérieure est éjectée vers l’extérieur à travers l’aqueduc (couleur vert-jaune) puis la tuyère (couleur jaune). Ceci parce que l’air comprimé enfermé dans la bouteille inférieure remonte par le conduit aéroduc (couleur bleue) jusqu’à la surface de l’eau pour chasser celle-ci vers le bas.

On remarque que, dans la zone de liaison des goulots, les deux fluides (l’air et l’eau) se croisent en sens inverses, chacun dans son tuyau.

Ce principe de fonctionnement offre l’avantage de stocker l’eau en partie haute de la fusée, disposition très favorable à la stabilité aérodynamique.
En effet, contrairement à une idée bien ancrée en nous, une fusée qui grimpe vers le ciel est plus stable lorsque son Centre des Masses se situe le plus haut possible (voir Le paradoxe de l’archer).

Au demeurant, le Centre des Masses d’une fusée se déplace continuellement pendant sa phase de propulsion (à mesure que la fusée expulse son eau, dans notre cas). On est donc contraint, pour le dimensionnement des ailettes d’empennage, à considérer le Centre des Masses dans sa position la plus défavorable, c-à-d celle située le plus en arrière (le plus bas).
Ce positionnement le plus arrière se produira parfois à vide sur nos fusées à flux d’air inversé à étage unique.(voir ci-dessous "Déplacement du Centre des Masses durant la phase propulsive..." )


Un autre intérêt de l’architecture à flux d’air inversé réside dans le fait que la masse d’eau est stockée dans un réservoir qui lui est propre.
Dans le cas d’une fusée à deux étages, ce confinement en réservoir propre évitera le joyeux mélange de l’air et de l’eau qui se produit dans le deuxième étage à l’arrêt du premier étage : La fusée vit alors, en effet, une phase assimilable à une période d’apesanteur (ou de pesanteur négative). Durant cette phase, il ne faut pas s’attendre à ce que les ergols restent sagement à la place où nous les voyons habituellement (le plus dense en bas, le moins dense en haut) : L’eau se met en bulle(s) dans l’air et ces deux fluides se disputent joyeusement le volume du réservoir au gré des efforts subit par la fusée (en particulier ceux dus au freinage de l’engin par l’atmosphère traversée).
Dans le cas d’une fusée classique, cette ‘‘déstratification’’ des ergols dans le réservoir conduit, lors du lancement du moteur, à un rapide dégazage de l’air sans effet d’expulsion de l’eau (l’air passant « par dessous » l’eau pour sortir).

Ce phénomène de déstratification se fait sentir de la même façon sur les lanceurs de satellites et oblige à l’utilisation de petites fusées à poudre produisant une accélération assimilable à une légère pesanteur artificielle. Cette pesanteur artificielle autorise la mise en route des pompes sans risques d’embolie gazeuse… (ces petites fusées sont visibles aux plans de séparation interétage).

Ce même phénomène de déstratification impose également aux constructeurs de fusées à eau à deux étages de programmer le départ du deuxième étage immédiatement en fin d’expulsion de l’eau du premier étage (c-à-d quelques dixièmes de secondes après le décollage) : L’expulsion de l’air résiduel assure alors la pesanteur artificielle nécessaire au début du fonctionnement du deuxième moteur… Cette précipitation « peu réaliste » induit il est vrai le meilleur gain en altitude pour ce deuxième étage.

Voir également notre page : Les techno-fusées , 

...ainsi que notre page FAI-monde  faisant état des réalisations, par d'autres fuséistes, de fusées à Flux d'Air Inversé...

Déplacement du Centre des Masses durant la phase propulsive d'une fusée à eau classique (courbe)

Une détermination pratique et ‘‘sensitive’’ de la position du Centre des Masses (CdM) de l’eau restante, pour chaque niveau d'eau, est possible.

Pour ce faire, on pourra tracer sur un bristol la courbe « des carrés des diamètres du réservoir d’eau », depuis la tuyère jusqu’à la surface libre du liquide avant le départ (en y incluant l’aqueduc, s’il en est un). Ces carrés seront rapportés à la hauteur (distance à partir de la tuyère) à laquelle les diamètres ont été mesurés (c'est à dire qu’on indiquera en x les hauteurs, et en y les carrés des diamètres à ces différentes hauteurs).
Une courte réflexion convaincra que le centre de gravité de l’aire de cette courbe est à la même hauteur (à la même abscisse x) que le centre de gravité de l’eau dans la fusée.

Comme le centre gravité de l’aire de la courbe peut être déterminé pratiquement en découpant cette aire dans le bristol et en la piquant avec une épingle, le déplacement de ce centre de gravité pendant la phase propulsive pourra être assez facilement déterminé : il suffira de soustraire une à une, d’un coup de ciseaux, des tranches de hauteur d’eau (d’un cm, par exemple) et de déterminer à l’épingle le centre de gravité de chaque aire ainsi définie…

En camping, le dessin de cette courbe d’évolution du CdM Total (eau + fusée à sec) peut se faire par la méthode graphique de composition de deux masses, pour chaque hauteur d’eau restante (par combinaison avec le Centre de Gravité de la fusée à sec). Cette méthode graphique, très pratique, était déjà utilisée par les constructeurs des cathédrales.

Ainsi procédera-t-on, sur la table de camping, pendant les vacances.

Le même calcul est évidemment faisable, le reste du temps, sur ordinateur. Ce doux compagnon dessinera sans effort la courbe de l’évolution du CdM de l’eau restante et celle de l’évolution du CdM Total en fonction de la hauteur d'eau restant dans la bouteille.

Voici par exemple ces courbes lors de la phase propulsive d'une fusée de 0,5 L (en rouge et bleu dense). La hauteur d'eau restante (qui sert d'abscisse) est rappelée sous forme d'une droite de coefficient directeur -1 (en bleu clair), on verra pourquoi :

La courbe du CdM Total arbore une forme en S, moins marquée cependant ici pour ce volume de 0,5 litres.

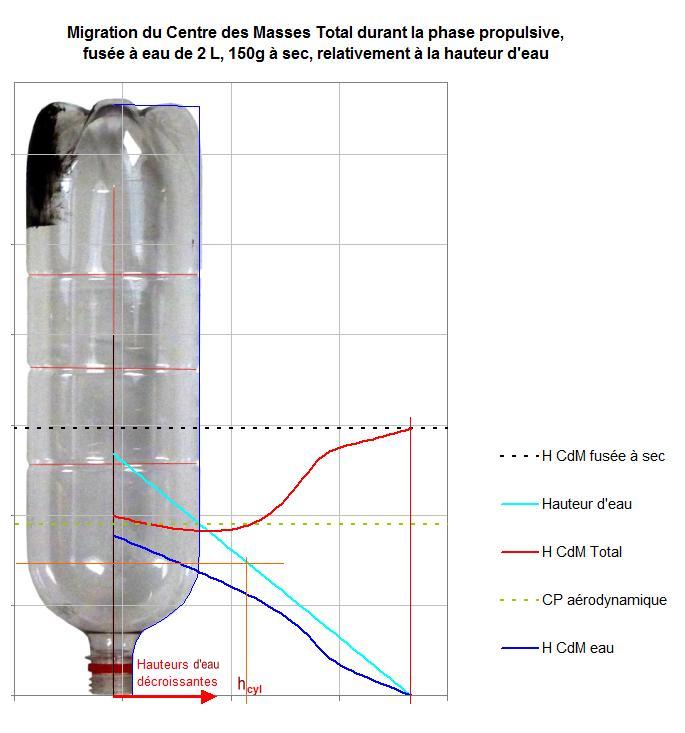
Mais pour le volume de 2 litres, le S est plus marqué :

Le méandre bas du S est souvent, sur les fusées de base, cause d'une phase d’instabilité transitoire, remarquable à une brusque (mais unique) inflexion de la trajectoire, du moins lorsque le Centre de Portance se situe au niveau de ce méandre. Dans ses ouvrages, le précurseur Jean-Paul Soulard présente des photographies de ces inflexions typiques…

La position la plus basse du CdM est donc celle qu’on doit prendre en compte pour le dimensionnement des ailettes.

La lecture des courbes se fait de gauche à droite : À gauche toute l'eau réside encore dans le réservoir, à droite la fusée est à sec.

L'analyse de ces courbes (référencées ici à la hauteur d'eau restante) est fort instructive pour qui s'intéresse à la physique. Exerçons nous-y sur le réservoir de 2 litres présenté ci-dessus :

Dans sa portion de droite (en fin de propulsion), la courbe bleu dense illustrant la hauteur du CdM de l'eau restant est un segment de droite de coefficient directeur moitié de celui de la courbe bleu clair puisque le goulot de la bouteille est un cylindre (le CdM des cylindres d'eau restant dans le goulot étant à la moitié de leur hauteur).

Lorsque la surface libre de l'eau est dans la grande partie cylindrique du réservoir (au-dessus de l'horizontale orange), la courbe bleu dense n'est pas linéaire.

On peut démontrer facilement que la courbe du l’évolution du CdM Total (en rouge) présente nécessairement une tangente horizontale au point où elle coupe la droite bleu clair.

Le choix de prendre, comme nous l'avons fait ci-dessus, la hauteur d'eau comme abscisse permet de simplifier la détermination des courbes, en s'affranchissant de la partie "mécanique des fluides" du phénomène. Mais dans la pratique, la hauteur d'eau dans le réservoir ne diminue pas régulièrement durant la phase propulsive (du fait de la décroissance de la vitesse d'éjection et du fait de la variation de diamètre de la surface libre de l'eau). Aussi est-il est plus réaliste d'utiliser le temps comme abscisse.

Une prise en compte de la décroissance de vitesse d'éjection (basée sur la  décroissance adiabatique de la pression, sur l'accélération de la colonne d'eau, ainsi que sur la Traînée atmosphérique pour un Cx type de 0,4 appliqué à la section de la bouteille),  de même qu'une prise en compte des variations de sections de la bouteille, permettent de référencer au temps les trois courbes déjà présentées (calculs effectués en Mécanique des Fluides Stationnaire). Ce changement de référence amène une modification de la forme  de ces courbes : 

L'effet de la décroissance de la vitesse d'éjection tout au long de la propulsion est d'espacer les abscisses dans la partie droite des courbes (la baisse d'eau se faisant moins rapide à mesure que la pression descend), mais la modification la plus nette des courbes est due à la simple diminution des sections de la bouteille en fin de propulsion (les derniers centimètres d'eau représentant peu de volume, leur éjection est effectuée beaucoup plus vite, comme cela se voit sur la courbe bleu clair) : Ce phénomène contracte tant (horizontalement) la courbe rouge dans sa partie droite qu'elle en perd sa forme de S.

Finalement, les courbes que l'on obtient en référence au temps sont celles que l'on verrait en observant les courbes dessinées en référence à la hauteur d'eau restante (graphe précédent) mais en  arrondissant le papier qui porte ses courbes (globalement du fait de la détente adiabatique de l'air et localement beaucoup plus dans la partie droite, du fait de la réduction des sections de la bouteille)...

Les courbes pointillées représentent l'évolution des trois mêmes paramètres sur une fusée maintenue au banc d'essais (l'accélération sur la colonne d'eau reste celle de la pesanteur et la Traînée n'existe pas).

Remarquons que dans les deux cas (vol calculé et "essai au banc" calculé) la tangence horizontale de la courbe rouge à son croisement avec la courbe bleu clair existe toujours car c'est un phénomène physique indépendant du temps.

Bernard de Go Mars ! Retour à l'accueil