DENSITÉ CRITIQUE
Densité de matière qui produirait un univers plat, dénué de toute courbure et égale à 3 atomes d'hydrogène par cm3. Un univers ayant une densité critique n'arrêterait sa dilatation qu'après un temps infini. Un univers ayant une densité supérieure à la densité critique aurait une courbure positive et s'effondrerait sur lui-même dans le futur, on dit aussi qu'il est fermé. Un univers ayant une densité inférieure à la densité critique aurait une courbure négative et une expansion éternelle, on dit aussi qu'il est ouvert. Les observations donnent notre univers comme étant ouvert.
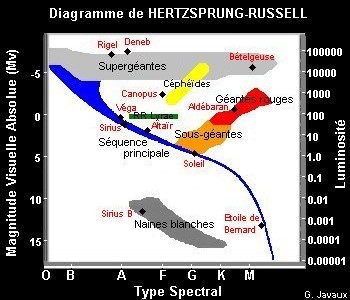
DIAGRAMME DE HERTZSPRUNG-RUSSELL
La lumière des étoiles nous fait parvenir un message brouillé et complexe. Pour en démêler les arcanes, les astronomes recourent à un outil mis au point dans les premières années du XXe siècle par Ejnar Hertzsprung (1905) et indépendamment par Henry Norris Russell (1914). Il s'agit d'un diagramme dans lequel les points représentatifs d'un ensemble d'étoiles sont placées en fonction de leur couleur, température superficielle ou type spectral (qui correspondent aux abscisses) et de leur luminosité ou de leur magnitude absolues ou apparentes (en ordonnées).
DISTANCE
Les astronomes entendent par le mot distance, quelquefois une ligne droite, quelquefois un angle ou un arc de cercle mesuré sur la sphère céleste, ce que l'on peut préciser alors en parlant de distance angulaire; mais le contexte détermine généralement cette signification de manière qu'il n'y a jamais d'équivoque.
Lorsqu'il s'agit de la distance d'un astre à la Terre, c'est une ligne droite tirée du centre de l'astre au centre de la Terre. Il en est souvent de même de la distance d'un astre au Soleil. S'il s'agit de la distance mutuelle de deux astres, ou d'un astre à un point quelconque du ciel elle est mesurée par l'angle que forment entre elles deux lignes droites, tirées du centre de chacun de ces astres, à la Terre, ou par l'arc de cercle compris entre ces deux lignes. La mesure de cette distance est aussi quelquefois un arc de cercle compris entre les deux cercles de déclinaison ou de latitude, qui passent par les centres des deux astres.
– En astronomie, les distances sont rapidement faramineuses :
Différentes méthodes utilisées aujourd'hui pour mesurer la distance des étoiles :
1. L’écho radio et laser : Pour mesurer la distance de la Terre aux satellites, y compris notre satellite naturel, la Lune, on peut utiliser la technique de l'écho radar, ainsi que du faisceau laser : connaissant la vitesse à laquelle chemine les ondes radio ou bien la lumière du laser, il suffit pour mesurer la distance nous séparant du satellite, de calculer le temps mis par l'onde pour aller jusqu'au satellite et en revenir.
2. La méthode des parallaxes : Pour les étoiles les plus proches de la Terre, les astronomes emploient la méthode des parallaxes
– distance Terre-Lune : 384 000 km
– distance Terre-Soleil : 149 597 870 km
– distance Terre-Pluton : 5 766 000 000 km
– l'Unité Astronomique (UA) : c'est la distance Terre-Soleil = 149 597 870 km
– l'Année-Lumière : c'est la distance parcourue par la lumière en un an, à la vitesse de 299 792 km/s = 63 239,8 UA
= 9 460 536 000 000 km
– le Parsec : 206 264,8 UA = 30 856 775 000 000 km
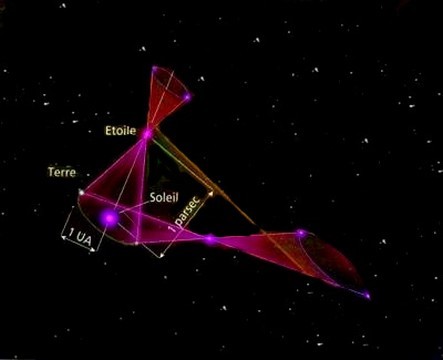
Dans son grand tour annuel autour du Soleil, la Terre nous emporte, modifiant légèrement notre angle de vue du ciel.
En particulier, les étoiles les plus proches de la Terre ne semblent pas au même endroit du ciel si on les regarde à 6 mois de différence. Et si on observe leur mouvement durant 12 mois, on constate qu'elles accomplissent un petit cercle dans le ciel, sur la toile de fond formée par les champs d'étoiles plus lointaines.
La mesure du déplacement apparent de l'étoile, appelée parallaxe, est mesurable. Le schéma ci-dessus vous permet de constater que plus une étoile est proche de nous et plus l'angle de sa parallaxe est important. A l'inverse, plus une étoile est éloignée et plus sa parallaxe est faible, difficilement mesurable
Les astronomes connaissent bien la distance Terre-Soleil (= 1 Unité Astronomique = 149 597 870 km) : ils peuvent alors calculer sans problème la distance Terre-étoile, grâce au théorème de Pythagore.
Au passage, rappelons que c'est cette méthode qui a permis de définir l'une des unités de mesure employées en astronomie : le Parsec. Le Parsec est la distance depuis laquelle le rayon de l'orbite terrestre est vu sous un angle d'une seconde d'arc.