II- Quadrature du cercle
Il s'agit de l'un des plus célèbres problèmes de la géométrie. Il a obsédé les mathématiciens durant plus de 2000 ans.
1) Quelques exemples

Calculs
|
Aire du cercle: |
p . r² |
|
Aire du carré: |
a² |
|
Quadrature: |
a² = p . r² |
|
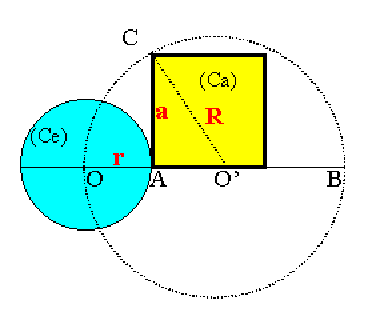
Évaluons a à partir de l’angle AO’C |
a = f(a ) |
|
sin (a ) = |
a / R |
|
cos (a ) = |
(R-r) / R |
|
sin² (a ) + cos² (a ) = |
1 |
|
(a / R)² + ((R-r) / R)² = |
1 |
|
a² + (R-r)² = |
R² |
|
a² = |
R² - (R-r)² |
|
Égalons les aires |
|
|
p . r² = |
R² - (R-r)² |
|
|
R² - R² + 2Rr - r² |
|
p = |
(2R - r) / r |
|
Revenons à la figure |
|
|
p = |
AB / OA |
Autrement dit
Il suffit de construire AB et OA dans le rapport p
On tourne en rond !..
2) Solution
Aristophane
(vers 444 - 380 av. J.-C.)
Première indication du problème:
"Avec une règle, je vais donner la forme du carré au cercle"
Les Grecs
croyaient avoir trouvé
même si leurs résultats n'étaient que de bonnes approximations.
On s'est vite rendu compte que c'était extraordinairement difficile,
voire impossible.
Nicholas de Cusa
(1404-1464),
cardinal et savant renommé,
avance que 3,1423 est la valeur exacte de p.
Joseph Scalinger
tente aussi de résoudre le problème.
Toutes ses tentatives seront réfutées par Viète.
Thomas Hobbes
(1588-1679),
dont les tentatives furent réfutées par John Wallis,
au prix de violentes disputes entre les deux hommes.
Jacob Marcelis
vers 1700, pense avoir résolu la question. Sa valeur exacte de ðp était:
3 x 1 008 449 087 377 541 679 894 282 184 894 / 6 997 183 637 540 819 440 035 239 271 702.
Edwin Goodwin
en 1897, publie quasiment un livre sur "une nouvelle vérité mathématique".
L'ouvrage passe la première lecture
et se trouve réfuté par C.A. Waldo en deuxième visée.
Lindemann
en 1882 démontre que p est transcendant.
Il ne peut satisfaire aucune équation algébrique à coefficients rationnels.
Il n'est qu'une suite infinie de termes.
Or, comme tout nombre construit à l'aide du compas et de la règle satisfait à une équation algébrique,
la quadrature du cercle est impossible.
3) Conclusion
Durant des siècles, on s'acharnera sur ce problème. On trouvera bien quelques méthodes mais faisant toujours appel à d'autres instruments que ceux autorisés. Ce n'est qu'à la fin du XIXe siècle, grâce aux travaux du mathématicien allemand Carl Louis Ferdinand Von Lindemann (1852-1939), que sera enfin démontrée l'impossibilité de la quadrature du cercle.