Le Nombre d'Or.
Partie 2 : Architecture et monuments.
Il suffit d'inscrire un pentagone étoilé à l'intériur d'un pentagone régulier pour faire tout naturellement apparaître le nombre d'or. Il est présent également dans le dodécaèdre et l'iconstruisit par la divion d'une droite en ce qu'il appelail « moyenne et extrême mesure ». Chacun des rapport AQ / QD, AP / BC est égal à ½ (1+5),soit environ 1,618.les grecs le dèsignaient gènèralement par la lettre ? (ou parfois ?). Un « rectangle d'or », dont les côtés suivent les proportions du nombre d'or, peut donc être découpé en un carré et un autre rectangle de même forme. Et on peut ensuite répéter le processus à l'infini. Les sommets ainsi formés peuvent servir au tracé d'une spirale équiangle: en réalité, la spirale ne touche pas tout à fait les côtés du rectangle.
b- Unités de mesures et instruments.
Pour calculer des mesures avec le nombre d'or, on utilise des instruments de mesure utilisés par les bâtisseurs romans: la canne des bâtisseurs, la quine des bâtisseurs, l'instrument articulé à 5 branches, l'équerre des arpenteurs égyptiens, la corde à 12 coudées et le niveau et le fil à plomb. Lorsqu'on veut évaluer une longueur on se sert souvent, soit de la main, soit du pied, soit d'enjambées; par exemple la main qui donne l'empan et permet la mesure d'une petite longueur comme celle d'une table. Pour les mesures, l'élément de base est la ligne. La ligne vaut 2,25 mm. Le pouce vaut 12 lignes soit 2,7 cm. La paume vaut 34 lignes soit 7,64 cm c'est 1/? au carré. Le palme vaut 55 lignes soit 12,36 cm c'est 1/ ?. L'empan vaut 89 lignes soit 20cm c'est 1. Le pied vaut 144 lignes soit 32,36cm c'est ?. La coudée vaut 233 lignes soit 52,36cm c'est ? au carré. La toise et le pouce ne sont pas toujours exprimés en fonction du nombre d'or mais pourraient l'être puisque la toise vaut 6 pieds soit 194,16cm et le pied vaut 12 pouces de 12 lignes.
Exemple: 6 coudées de 0,5236m correspond à 3,1416...=? 3 pieds de 0,3236 valent sensiblement un métre. La paume, le palme, l'empan, le pied et la coudée (les cinq éléments de la quine des bâtisseurs) se réfèrent à des dimensions humaines et en même temps au nombre d'or ?, la divine proportion.
1-Tracé l'ogive idéale.
Soit l'ouverture AB.O est le milieu de AB. En B,élever la perpendiculaire
By à AB. Tracer un arc de cercle de centre B,de rayon BO,qui coupe By
en D. Tracer un arc de cercle de centre O, de rayon OD,qui coupe AB en
C. Tracer un arc de cercle de centre C, de rayon CA,qui coupe la médiatrice
de AB en E. Par symétrie par rapport à l'axe OE,on détermine l'arc EB
On a construit l'arc brisé (ogive idéale)AEB.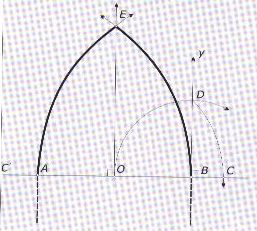
2-Tracé l'arc brisé tiers-point.
Soit l'ouvreture AB. Partager le segment de droite AB en trois parties
égales(1-08 page 21) AC=CD=DB=AB/3 Tracer l'arc de cercle de centre C
de rayon CB. Tracer l'arc de cercle de centre D de rayon DA. Ces deux
arcs de cercle se coupent en E. AEB est l'arc brisé tiers point.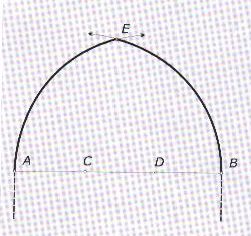
3-Tracé l'arc brisé adapté au plan carré.
Soit le carré fondamental donnant l'ouverture de l'arc AD. O est le centre
du carré. Tracer l'arc de cercle de centre D rayon DO qui coupe AD en
E. Tracer l'arc de cercle de centre A de rayon AO qui coupe AD en F. Tracer
l'arc de cercle de centre F de rayon DO puis l'arc de cercle de centre
E de rayon DO. Ces deux arcs de cercle se coupent en G sommet de l'arc
brisé AGD.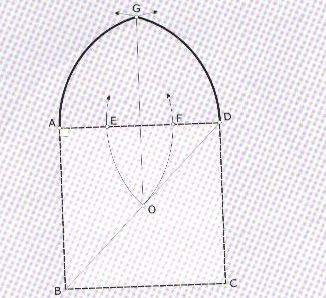
4-Tracer l'arcs brisés,tracé avec la corde à noeuds.
Soit AB = 8u (u pour ''unité'' comme la coudée,le pied ,la paume...)
et E milieu de AB. Placer les points C et D tels que AC = 3u et CD = 2u.
Tracer un arc de cercle de centre C de rayon = 5u. Tracer un arc de cercle
de centre D de rayon = 5u. Ces deux arcs de cercle se coupent en F. De
F mener la la paralléle AB qui coupe la perpendiculaire à AB en A au point
G pareillement on obtient le point H. Le rectangle AGHB est un rectangle
d'or. 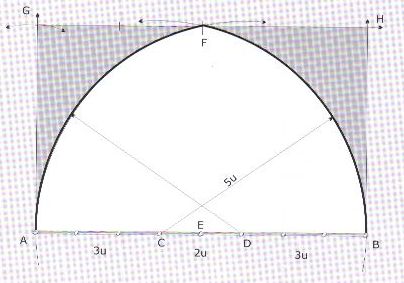
d)Autres exemples de monuments.
De plus, le nombre d'or a intervenu dans beaucoup d'autres monuments historiques comme les pyramides égyptiennes ou encore un grand monument appelé la Géode qui a été construit a l'aide du nombre d'or. Le Parthénon s'inscrit dans un rectangle doré, c'est-à-dire tel que le rapport de la longueur à la hauteur était égal au nombre d'or. Sur la figure : DC/DE = . Sur la toiture du temple, GF/GI = Le rectangle GBFH est appelé rectangle Parthénon.