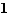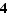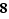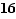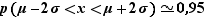La loi normale

  Deux exemples

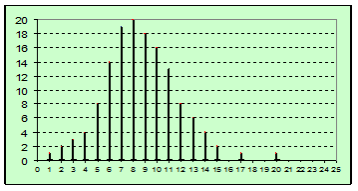
Il n’y a, à priori, aucun rapport entre un problème de mémoire et le lancer de pièces de monnaie.

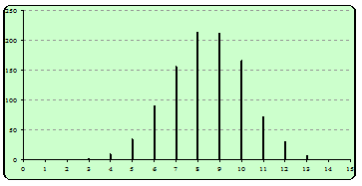
Mais leurs diagrammes en bâton ont tous deux la même allure générale :

    •quasi symétrie autour de la moyenne

    •une forme proche d’une courbe en cloche

De nombreuses séries statistiques, comme les deux exemples, possèdent une distribution proche de la courbe en cloche

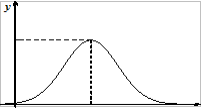
           Courbe en cloche

Une série statistique dont la distribution est une courbe en cloche suit une loi appelée loi normale de Gauss

La courbe en cloche représente la fonction de densité de la loi normale

  La loi normale

La loi normale est parfaitement définie par deux paramètres, sa moyenne μ et son écart-type σ

On la note N(μ,σ² )

Mais son expression algébrique est trop complexe pour pouvoir être utilisée. Tous les calculs se feront donc  à la calculatrice.

le nombre  σ² est appelé variance

Attention : au terme  σ² !

Par exemple : une loi normale N(3,16) est de moyenne μ = 2 et d'écart-type σ = 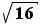  = 4

Cette notation peut être source d'erreurs car avec votre calculatrice vous utiliserer la moyenne μ et l'écart-type σ

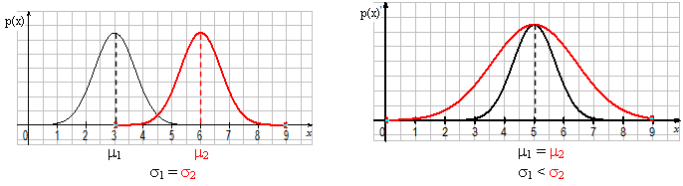
    •si on modifie la moyenne, la courbe se translate sans se déformer

    •si on modifie l'écart-type, la courbe se modifie : plus l'écart-type est petit, plus la courbe se resserre autour de la moyenne

3) Approximation d'une série statistique par une loi normale

Si une série statistique peut eptre approximée par une loi normale. On calcule sa moyenne 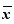  et son ecat-type σ .

La loi normale est moyenne μ = 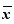   et de variance v =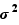  

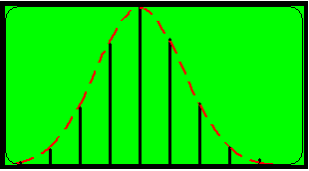
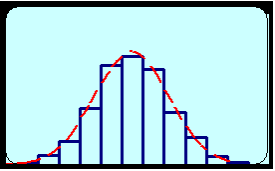
cas d'une série à caractère discret                               Cas d'une série en classe

un exemple sur EXCEL ici                                      Un exemple sur EXCEL ici

4) calcul de probabilité avec la loi normale

rappel de statistique à caractère continu

Prenons par exemple, le poids en kg d'une population d'adultes, entre 40 et 90 kg.

On pourrait ranger la population suivant cet ordre:

40kg, 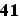  kg,.................,90kg (51 poids différents possibles)

Mais avec une balance au cg près :

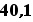40kg,   kg, 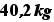  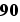.............,   kg (500 poids différents possibles)

Et rien ne nous empêche d'imaginer des balances au mg près  ou encore plus précises.

Conclusion : Il n'est pas possible de ranger la population suivant tous les poids possibles, il y en a beaucoup trop.

C'est pour cette raison que l'on range la population suivant des intervalles de poids appelés classes.

Pour faire les calculs on utilisera les ECC :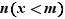  

Par exemple pour calculer le nombre de personnes ayant un poids compris entre 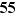  et   :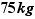

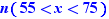  = n(x < 15)    n(x < 55) =   ( en fréquence 0,74)

Utilisation de la loi normale

Les paramètres de la série des poids sont :

moyenne : 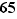  kg

variance :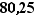  

écart-type : 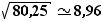   kg

On utilisera la loi normale N(65 ; 80,25)

Comme dans le cas d'une serie statistique à caractère continu on n'utilise pas la fonction de densité : p(x=m) mais p(x < m) ou p( 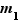  < x <   )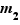

Avec la calculatrice on calculera

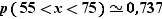
5) L'intervalle [μ 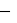  kσ, μ + kσ]

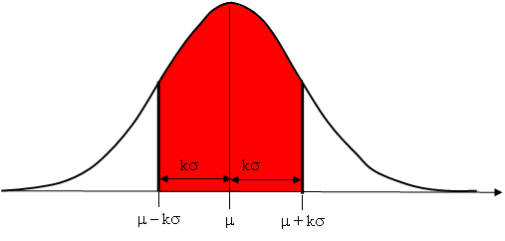
Quelque soit la loi normale on a toujours :

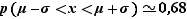
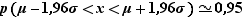
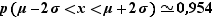  (proche de 0,95)

vérifier ces résultats sur EXCEL ici

5) Théorème de De Moivre Laplace

Une loi binomiale  B(n,p) peut être approximée par une loi normale de même moyenne et de même écart type

moyenne de la loi binomiale : 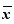  = np

variance  de la loi binomiale : v =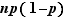  

écart type de la loi binomiale ; σ =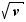  

La loi normale qui approxime cette loi binomiale est :

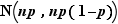
L'approximation est d'autant meilleure que :

    n est grand

    p est proche de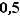  

Vérifiez le ici