Une conséquence immédiate de la définition 4 est la suivante:
Proposition 1: Soit G(X,Y) l'ensemble des propositions analytiquesdont
le sujet est l'élément X; si 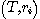 est la totalisation d'une unité d'éléments et si M
est un élément tel qu'il existe au moins un jugement analytique
exprimé par la proposition est la totalisation d'une unité d'éléments et si M
est un élément tel qu'il existe au moins un jugement analytique
exprimé par la proposition  , la formule , la formule
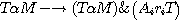
établit une bijection
entre  et le sous-ensemble et le sous-ensemble 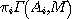 constitué par les propositions de constitué par les propositions de  vérifiant (ii) c'est-d-dire telles que vérifiant (ii) c'est-d-dire telles que
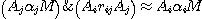
Le diagramme de la figure 7 illustre cette proposition.
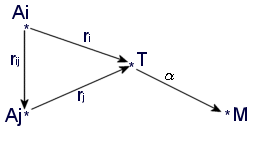
Figure 7: Diagramme de la proposition 1
On voit en effet que toute
proposition  , en conjonction avec une proposition , en conjonction avec une proposition 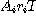 permet d'affirmer l'existence d'un jugement analytique pour le sujet permet d'affirmer l'existence d'un jugement analytique pour le sujet 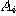 . En effet, son concept est contenu dans celui de M puisqu'il est contenu
dans celui de T qui par hypothèse est contenu dans celui de M. On peut
donc lui associer un élément . En effet, son concept est contenu dans celui de M puisqu'il est contenu
dans celui de T qui par hypothèse est contenu dans celui de M. On peut
donc lui associer un élément 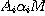 de de 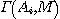 qui vérifie(ii). qui vérifie(ii).
Réciproquement, si
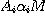 est une famille de propositions qui vérifie (ii)alors,
d'après (iii), il existe une proposition unique est une famille de propositions qui vérifie (ii)alors,
d'après (iii), il existe une proposition unique
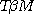 exprimant un jugement analytique tel que exprimant un jugement analytique tel que
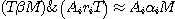
Il s'ensuit, en raison de
l'unicité de 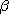 que que 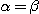 et la proposition est établie. et la proposition est établie.
L'intérêt de
cette proposition est le suivant: tout jugement analytique  exprimant que le concept de T est contenu dans le concept de M produit,
étant donnée la construction de T, une famille de jugements analytiques
entre chacun des exprimant que le concept de T est contenu dans le concept de M produit,
étant donnée la construction de T, une famille de jugements analytiques
entre chacun des 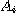 et M exprimant que le concept de chacun des et M exprimant que le concept de chacun des  est contenu dans le concept de M. Par exemple, l'appartenance de la famille
F à la branche B induit l'appartenance de chaque personne de la famille
à cette branche. En d'autres termes, si T a M exprime une propriété
du tout T cette propriété est transmise à tout est contenu dans le concept de M. Par exemple, l'appartenance de la famille
F à la branche B induit l'appartenance de chaque personne de la famille
à cette branche. En d'autres termes, si T a M exprime une propriété
du tout T cette propriété est transmise à tout 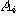 .. Inversement, pour que des énoncés de propriété
des éléments .. Inversement, pour que des énoncés de propriété
des éléments 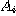 passent au tout T il faut et il suffit qu'ils soient relatifs au même
ensemble de propriétés d'une part et qu'ils vérifient
(ii) d'autre part, c'est-à-dire qu'ils «respectent»
les relations constitutives de l'unité d'éléments. Considérons
l'exemple simplifié de la figure 8. passent au tout T il faut et il suffit qu'ils soient relatifs au même
ensemble de propriétés d'une part et qu'ils vérifient
(ii) d'autre part, c'est-à-dire qu'ils «respectent»
les relations constitutives de l'unité d'éléments. Considérons
l'exemple simplifié de la figure 8.

Figure 8: Famille et branche h
|

