To this end it will suffice to consider that an object is "present
to the mind"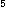 if and only if this mind "forms" its eidetic structure.
Indeed, since this structure is included (that is to say present)
in each perceptual judgement (mental semantic network) of every
member of the community, we automatically obtain its "presence
to the mind." For every perceiving entity there is a one to
one correspondence between perceived objects of the world and a
set of connected relational structures of if and only if this mind "forms" its eidetic structure.
Indeed, since this structure is included (that is to say present)
in each perceptual judgement (mental semantic network) of every
member of the community, we automatically obtain its "presence
to the mind." For every perceiving entity there is a one to
one correspondence between perceived objects of the world and a
set of connected relational structures of 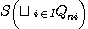 . This point of view agrees perfectly with the principle of the "identity
theory" enunciated by Jackendoff . This point of view agrees perfectly with the principle of the "identity
theory" enunciated by Jackendoff 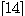 : "the distinction between mental and physical events is purely
one of mode of description." : "the distinction between mental and physical events is purely
one of mode of description."
The morphisms between eidetic structures are naturally interpreted
as relations between world objects. Finally this modelization consists
in substituting for the exterior world, considered as
a "vague" category with objects and relations between
these objects, tile precise category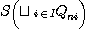 with the aid of a "metaphorical functor" supported by the mechanism
of the perception of the exterior world itself. This functor is
created, so to speak, from the very fact of the ierception of objects
and of their relations. with the aid of a "metaphorical functor" supported by the mechanism
of the perception of the exterior world itself. This functor is
created, so to speak, from the very fact of the ierception of objects
and of their relations.
The objects of the
world are, most of the time, present to the mind simultaneously
with ether objects, if only through their own constituent parts
with which they are related. In other vords the objects participate
in what Peirce calls a "phaneron" (synonymous for him
with "phenomenon"). The phaneron is "the collective
total of all that is in any way or in any sense present o the mind,
quite regardless of whether it corresponds to any real thing or
not" (8, CP 1 2841. recording to the previous hypothesis, it
follows that a phaneron can be produced by the perception of a set
of related objects of the exterior world, or internally constituted
by the mind which associates their eidetic structures already memorized,
or by a combination of both. These eidetic structures are combined
by means of their possible morphisms. (Changeux speaks of "associative
properties of mental objects.") Again using Category Theory,
we will build the formal framework 'or dealing with the phaneron
(phenomenology), that is to say the structure of all that can be
present to the mind.
Before that, we
will establish a reduction theorem and give a few definitions (in
keeping with ;he philosophical speculations and the formal intuitions
of C. S. Peirce) which permit us to describe more easily the phaneron
and the relations between phanerons.
DEFINITION 7. Let 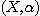 be a relational structure of type n on base set X and be a relational structure of type n on base set X and 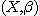 a relational structure of type m on the same base set; we define
the relative product of (X, a relational structure of type m on the same base set; we define
the relative product of (X, ) by ) by 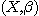 , and we call , and we call 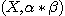 the relational structure of type n + m- 2 defined by the following subset
of the Cartesian product set of : the relational structure of type n + m- 2 defined by the following subset
of the Cartesian product set of :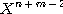
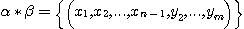 such that there exist such that there exist 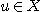
such
that 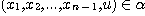 and and 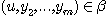 . .
DEFINITION 8. A relational structure 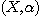 is relatively decomposable on a set is relatively decomposable on a set 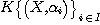 of relational structures if of relational structures if 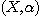 is the relative product of a set of relational structures of
K is the relative product of a set of relational structures of
K
DEFINITION 9. A relational structure 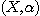 of type n is relatively reductible on k if and only if of type n is relatively reductible on k if and only if 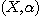 is relatively decomposable on a set is relatively decomposable on a set 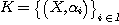 of relational structures on K of type smaller than n. If a relational
structure is not relatively reductible on K it is relatively irreductible
on K. of relational structures on K of type smaller than n. If a relational
structure is not relatively reductible on K it is relatively irreductible
on K.
It is easy to establish that
every relational structure of a type equal to 3 or smaller than
3 is relatively irreductible within any domain.
THEOREM 1. Let 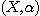 be a relational structure of type be a relational structure of type 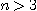 and and 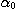 a set of the same cardinality as a set of the same cardinality as  ; we consider ; we consider 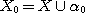 and the relational structure and the relational structure 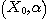 to be of type n defined on to be of type n defined on 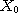 by the n tuples of a. Then by the n tuples of a. Then 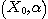 is relatively reductible on a set of relational structures of
type 3. is relatively reductible on a set of relational structures of
type 3.
PROOF (n = 4): Let 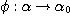 a bijection of a bijection of  onto onto 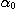 . We call . We call 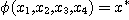 the corresponding element of the corresponding element of 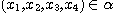 . We define two triadic relations on . We define two triadic relations on 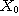 by: by:
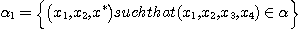
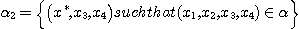 . .
We form the relative product 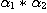 and let and let 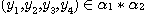 . .
There exists 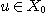 such that such that 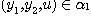 and and 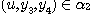 and there are and there are 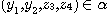 and and 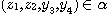 . .
Clearly, since 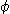 is a bijection and is a bijection and 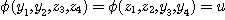 , we get , we get 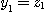 , , 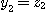 , , 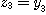 , , 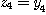 . Hence . Hence 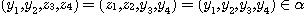 .We conclude that .We conclude that 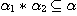 ; ; 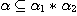 is obvious and we have is obvious and we have 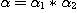 . .
There is no difficulty in extending this
proof to 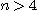 considering the considering the 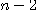 triadic relations defined as follows: triadic relations defined as follows:
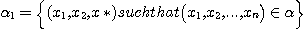
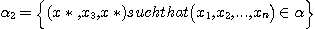
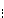
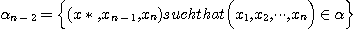
where 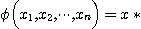 . The method used above is in accordance with the principles enunciated
by C. S. Peirce in [15]. . The method used above is in accordance with the principles enunciated
by C. S. Peirce in [15].
This reduction thesis6 proved differently
in terms of extensional logic by H. G. Herzberger  and in terms of intentional logic by R. W. Burch and in terms of intentional logic by R. W. Burch  seems to be in opposition to a well known result of W. V. O.
Quine (18) according to which every n adic predicate can be reduced
to a combination of dyadic predicates. This discussion has no place
in this work, but we note simply that it is, in our opinion, a difference
of viewpoint as to the importance accorded to the notion of "teridentity"
(see [17,19] and the article by R. W. Burch in this volume). seems to be in opposition to a well known result of W. V. O.
Quine (18) according to which every n adic predicate can be reduced
to a combination of dyadic predicates. This discussion has no place
in this work, but we note simply that it is, in our opinion, a difference
of viewpoint as to the importance accorded to the notion of "teridentity"
(see [17,19] and the article by R. W. Burch in this volume).
Now, the reduction theorem allows us
to describe every relational structure on X of type n by means of
the relative product of relational structures of type 1, 2 or 3,
called elementary relational structures. We call "monads"
the elements of relational structures of type 1 (1- tuples); we
call "dyads" the ones of type 2 (2- tuples) and "triads"
the ones of type 3 (3- tuples). Each monad corresponds to a simple
"quality of feeling," each dyad to an existent individual
or a fact, and each triad to a "concept, law or something expressible
by universal proposition." This is the empirical decomposition
of the phaneron into indecomposable elements many a time described
by Peirce.
If 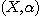 is an eidetic structure of an object of type is an eidetic structure of an object of type 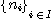 by introducing enough new individuals like by introducing enough new individuals like 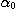 for every for every 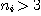 such that such that 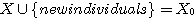 , we can consider that every object of the world is represented
in our model by a relational structure of , we can consider that every object of the world is represented
in our model by a relational structure of 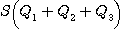 that is to say a relational structure of type {1, 2, 3}. But, considering
that the perceptual judgement which assembles n qualities
of feeling of an n- tuple assembles a fortiori all the k-
tuples (n < k) obtained erasing n- k of
these qualities of feeling, we define a special relational structure
of type { 1, 2, 3} as follows: that is to say a relational structure of type {1, 2, 3}. But, considering
that the perceptual judgement which assembles n qualities
of feeling of an n- tuple assembles a fortiori all the k-
tuples (n < k) obtained erasing n- k of
these qualities of feeling, we define a special relational structure
of type { 1, 2, 3} as follows:
DEFINITION 10. A relational structure 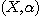 of type {1, 2, 3} on the set X with of type {1, 2, 3} on the set X with 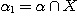 , , 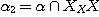 , , 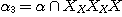 is a phenomenological structure of type is a phenomenological structure of type 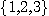 if the following conditions are fulfilled: if the following conditions are fulfilled:
(i) if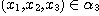 , then , then 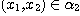 ,, ,, 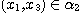 ,, ,, 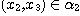
(ii) if 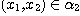 , then , then 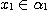 and and 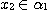
By combination of
(i) and (ii) we have:
(iii) if 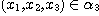 , then , then 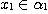 , , 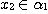 and and 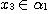
PROPOSITION 1. The relations R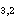 defined by the above condition (i) between defined by the above condition (i) between 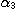 and and 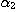 , R , R 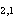 defined by defined by 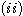 between between 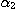 and and 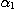 , , 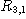 defined by (iii) between defined by (iii) between 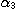 and and 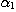 , define a category , define a category
called 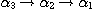 of which objects are
the of which objects are
the 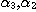 , and , and 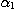 and the morphisms and the morphisms 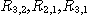 and the identities on and the identities on 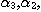 , and , and 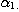
Indeed we have 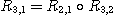 . Henceforth, we will represent the phenomenological structure
associated to an object of the world by . Henceforth, we will represent the phenomenological structure
associated to an object of the world by 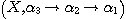 where X is a set and where X is a set and 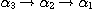 the category defined in Proposition 1. We recall that, if X and Y are two
sets, a functional correspondence between X and Y is a relation the category defined in Proposition 1. We recall that, if X and Y are two
sets, a functional correspondence between X and Y is a relation
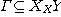 such that if such that if 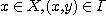 , and , and 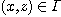 then then 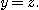
DEFINITION 11. Let
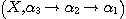 and and 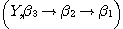 two phenomenological structures and two phenomenological structures and  a functional correspondence between X and Y; we consider the following sets: a functional correspondence between X and Y; we consider the following sets:
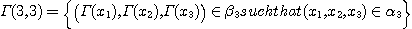
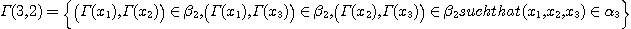
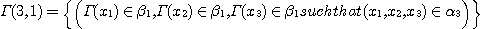
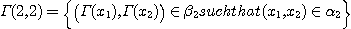
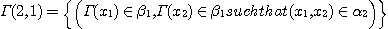
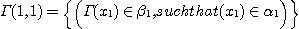
and
the corresponding relations (called elementary morphisms)
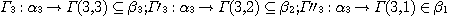
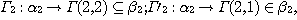
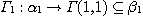
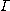 is called a phenomenological
morphism if is called a phenomenological
morphism if 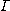 determines a functor of the category determines a functor of the category 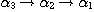 into the category into the category 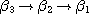 by means of the relations by means of the relations 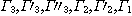 . .
For
instance, the functional correspondences r are such that we have
the following commutative diagrams which are phenomenological morphisms: |
