2.1 - Kinematics - questions

0 - What does Δ (delta) in for example Δx mean ?

1 - What is the difference between distance and displacements ?

2 - What is the difference between speed and velocity ?

3 - What is acceleration ?

4 - What is the average speed and velocity ?

5 - What is the instantaneous speed and velocity ?

6 - It is 20km from Lund to Malmo and a car drives from Malmo to Lund and then back to Malmo in 0.4 hours.
What is the average speed and velocity ?

7 - What is uniform motion and acceleration ?

8 - What is the SUVAT formulas for uniform acceleration ?

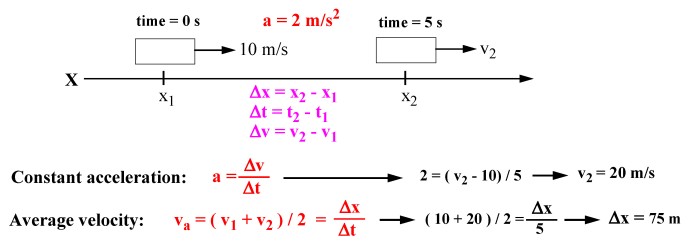
9 - A car travelling at 10 m/s accelerates at 2 m/s2 for 5s. What is its displacement ?

10 - A car is travelling at 10 m/s with uniform motion. What is its displacement after 5s ?

11 - Draw graphs of displacement versus time, velocity versus time and acceleration versus time for uniform motion.

12 - Draw graphs of displacement versus time, velocity versus time and acceleration versus time for uniform acceleration.

13 - How do you get velocity in a displacement-time graph and acceleration in a velocity-time graph ?

14 - How do you calculate the displacement in a velocity-time graph ?

15 - What can you calculate from the area in an acceleration-time graph ?

2.2 - Free fall motion - questions

16 - What is the velocity and acceleration if you drop something in vacuum ?

17 - What is the velocity and acceleration if you drop something in air ?

18 - You have two balls of the same size, one is empty and one if full of iron.
Which will fall fastest to the ground on the Moon ?
Which will fall fastest to the ground on the Earth ?

2.3 - Graphical representation of motion - questions

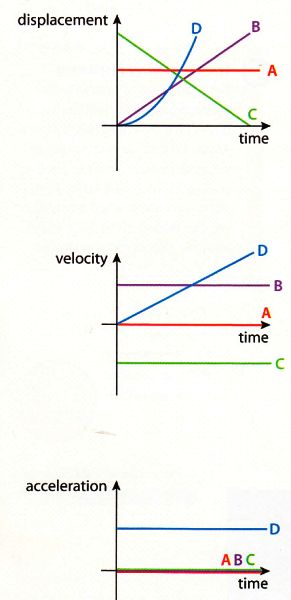
19 - What sort of motion do the lines called A describe ?

20 - What sort of motion do the lines called B describe ?

21 - What sort of motion do the lines called C describe ?

22 - What sort of motion do the lines called D describe ?

2.5 - Forces and dynamics - questions

23 - What does it means that the forces are balanced ?

24 - Draw a picture of a block on a slope with balanced forces.

25 - What are the equations for a block on a slope with balanced forces ?

26 - How do you calculate the force W (the weight) ?

2.6 - Newton's laws of motion - questions

27 - What is Newton's first law of motion ?

28 - Use Newton's first law to explain what happens to a rocket sent out in space after the rocket engine is turned off.

29 - Use Newton's first law to explain what happens to a car moving with a constant velocity.

30 - Use Newton's first law to explain what happens to a car if the engine is turned off.

31 - What condition is needed to have translational equilibrium ?


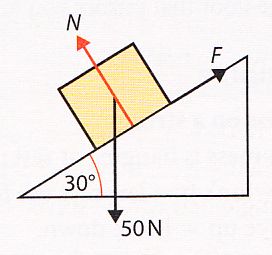
32 - The block above is in translational equilibrium. Calculate the forces.


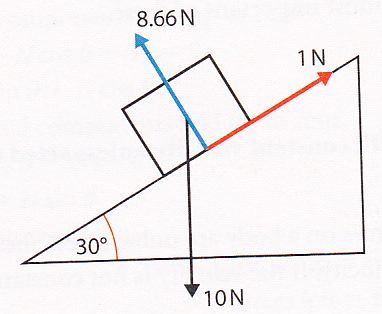
33 - The block above is not in translational equilibrium. Calculate the resulting force on the block.


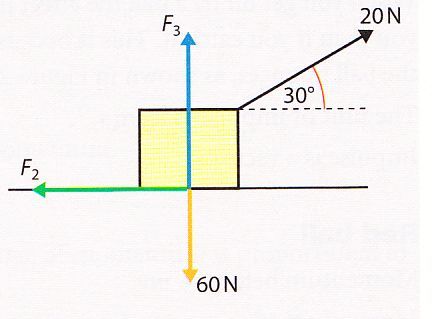
34 - The block above is in translational equilibrium. Calculate the forces.

2.7 - The relationship between force and acceleration - questions

35 - What is momentum ?

36 - What is impulse ?

37 - What is Newton's second law of motion ?

38 - A 500 kg heavy elevator is accelerating upwards with 1 m/s2. What is the tension in the cables ?

39 - A 500 kg heavy elevator is accelerating downwards with 1 m/s2. What is the tension in the cables ?

40 - Which of the following quantities are scalars and which are vectors: m, p, I, v, a, F, t ?

2.8 - Newton's third law - questions

41 - What is Newton's third law ?

42 - Apply Newton's third law on a box sitting on the floor !

43 - Apply Newton's third law on an object falling in the earths gravitational field !

44 - What does the law of conservation of momentum say ?

45 - The law of momentum conservation only works if the system is isolated, what does that mean ?

46 - Can you apply the law of momentum conservation to a ball hitting a wall ?

47 - Can you apply the law of momentum conservation to a ball hitting the wall of a spaceship ?


48 - Assume that the picture above shows an isolated system. Calculate v.

2.9 - Work, energy and power - questions

49 - What is work ?

50

51

52

53

54 - How can you calculate the work if the force is not constant ?

55 - What is energy ?

56 - Name a few different forms of energy !

57 - There is a law about energies. What does it say ?

58 - What is kinetic energy ?

59 - What is potential energy ?

60 - What is total energy ?

61

62 - What is an elastic collision ?

63 Calculate v1 and v2 in the following elastic collision: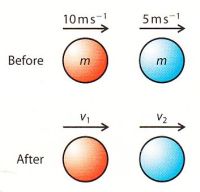

64 - What is power ?

65

66 - What is efficiency ?

67

2.10 - Uniform circular motion - questions

68 - What is the time period for circular motion ?

69 - What is the frequency for circular motion ?

70 - What is angular velocity ?

71 - What are the formulas for the centripetal force ?




2.1 - Kinematics

Δx = xfinal - xinitial so Δ mean that one take the difference between two values.

Displacement is a vector. Unit = m.
Distance is a scalar (a number), it is the length that has been travelled. Unit = m.

Velocity is a vector. It is defined as Velocity = displacement / time . Unit = m/s .
Speed is a scalar (a number). It is defined as Speed = distance / time . Unit = m/s .

Acceleration is a vector. It is defined as Acceleration = change of velocity / time . Unit = m/s2 .

Formula: a = (v - u) / Δt
where v is the velocity at time t1 and u the velocity at time t2 and Δt = t2 - t1

Average speed and velocity is when one averages over a long time (t). During this time the velocity and speed might go up and down.
The formula to use for the calculation is v = s / t where s is displacement if the velocity is calculated and s is distance if the speed is calculated.

Instantaneous speed and velocity is the speed and velocity at a specific moment in time. It has to be calculated with v = δx / δt , where v is the velocity or speed during a short time interval (δt) when the distance travelled in that time interval is δx.

It is 20km from Lund to Malmö and a car drives from Malmö to Lund and then back to Malmö in 0.4 hours.
The distance is then 40 km. The displacement is then 0 km. The speed is 40/0.4=100 km/h. The velocity is 0/0.4=0 .

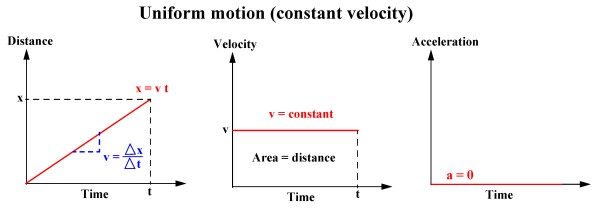
Uniform motion (or velocity) is motion when the velocity is constant (it does not change).
Uniform acceleration is motion when the velocity is not constant but the acceleration is constant. So the change of the velocity (=acceleration) is constant.


First look at the data booklet:










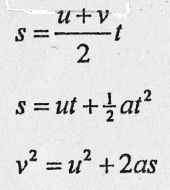
Uniform motion means that the velocity is constant and the acceleration is therefore zero. A graph of displacement versus time shows a straight line with its gradient being the velocity. A graph of velocity versus time is therefore a constant line and a graph of acceleration versus time is empty since the acceleration is zero.



Uniform acceleration means that the velocity is not constant but that the acceleration is constant. A graph of displacement versus time shows a parabola. A graph of velocity versus time is a straight line with its gradient being the acceleration. A graph of acceleration versus time is a constant line.



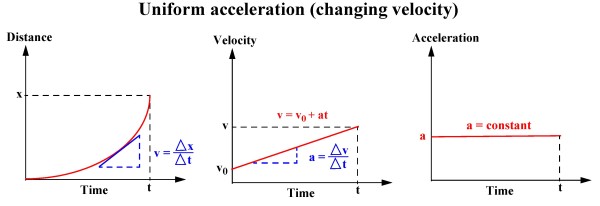
Draw the tangent to the curve at the time you want to get velocity or acceleration and calculate the gradient (slope) of the tangent. That is equal to calculating v = δS / δt and a = δv / δt .

The displacement can be calculated in a velocity-time graph because it is equal to the area under the graph.

The area under the curve in an acceleration-time graph give the change in velocity Δv = v - u.

2.2 - Free fall motion

The acceleration on the earth and in vacuum is a = g = 9.82 m/s. This means that the velocity if one drops something in vacuum is always increasing.

The acceleration on the earth and in air is a = g = 9.82 m/s. However, the air will cause a force from air resistance that will slow down the acceleration until it is eventually zero (if it can fall long enough). The velocity is then constant and will not increase anymore.

On the moon where there is no air the two balls will fall with a constant acceleration and hit the ground at the same time.
On the earth there is air resistance but if that is the same for the two balls they will also hit the ground at the same time.

2.3 - Graphical representation of motion

2.4 - Projectile motion

Only high level stuff

2.5 - Forces and dynamics

Balanced forces means that the sum of all forces is zero.

The force W (the weight) is calculated from W = m•g = mass x 9.81 (Unit: N)

If you have forgotten the value of g you can find it in the data booklet.

2.6 - Newton's laws of motion

Newton's first law of motion:

i) An object at rest stays at rest.
ii) An object in motion stays in motion with the same speed and direction,
iii) unless an external unbalanced force is acting on the object.



It is very important to understand the meaning of Newton's first law:
An object can keep on moving even if there is no force acting on it !
But it cannot change its velocity (accelerate) without an external force !

A rocket sent out in space will (after the rocket engine is turned off and after it has escaped the gravitational pull of earth), continue with the same speed and direction until it hits a star.

A moving car that has the engine turned off will no longer have its forces balanced. There will be no force created by the engine that turns the wheels and creates a friction force between the tires and the road. But the force from air resistance will still be there. So the velocity will slow down (there will be a de-acceleration) due to the air resistance force. The Newton's first law is NOT applicable since the forces are not balanced. However, after some time the car will be standing still and no air resistance force is then working on the car and now Newton's first law is applicable.

In order to have translational equilibrium all the forces on a body have to be balanced.


2.7 - The relationship between force and acceleration

Momentum is defined as the product of mass and velocity: p = m•v = mass x velocity (Unit: kg m/s or Ns)

Look at the data booklet:

Impulse is defined as the change of momentum: I = Δp = mvfinal - mvinitial (Unit: kg m/s)


Look at the data booklet:

Newton's second law of motion:

Look at the data booklet:

Version 1.
i) An unbalanced force acting on an object causes its momentum (p = m•v) to change.
ii) The rate of the momentum change is proportional to the force and will be in the same direction as the force

Look at the data booklet:

Version 2.
i) An unbalanced force acting on an object causes it to accelerate.
ii) The acceleration is proportional to the force and will be in the same direction as the force (F=a•m → a = F / m).
iii) The acceleration is inversely proportional to the mass (F=a•m → a = F / m).



Note that if the mass do not change, then the momentum change in version 1 is equal to a change of velocity which is the same thing as an acceleration. So version 1 covers the cases where both mass and velocity can change while version 2 only covers the case where the velocity is changing (which is most cases but not all).

Scalar: m , t
Vector: p, I, v, a, F

2.8 - Newton's third law

Newton's third law

i) If body A exerts a force on body B
ii) then body B will exerts a force on body A
iii) that is of the same size and opposite direction.




So the object will pull the earth up with a force that is equal to the force that the earth is pulling the object down. Since the earth is so big this small force on it is, however, insignificant.

The law of conservation of momentum:

Version 1
i) For a system of isolated bodies
ii) the total momentum (the sum of the momentum of all objects) is always the same.

Version 2
If something happens that change the momentum of the objects then pafter = pbefore

An isolated system is a system on which no external forces are working.

If a ball hits a wall, the ball and the wall is NOT an isolated system.
The reason is that the wall is attached to the ground and the ground is exerting strong forces on the wall.
So the law of momentum conservation cannot be used on a ball hitting a wall.

If a ball hits a wall floating in space, the ball and the wall is an isolated system.
So the law of momentum conservation can be used on a ball hitting a wall of a spaceship.

2.9 - Work, energy and power

Look at the data booklet:

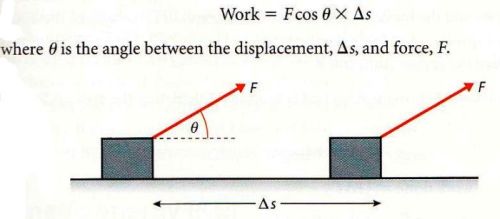
Work: W = F•Δs = Force x Distance moved in the direction of the force










If the force is not constant you can calculate the work as the area under a force-distance graph.

Example:

Energy is the capacity of a system to do work on other systems. Unit: Joule (J)

Some of the many forms that energy takes are:

  • Mechanical energy, which includes

- Potential energy, stored in a system.

- Kinetic energy, from the movement of matter.

  • Radiant or solar energy, which comes from the light and warmth of the sun.
  • Thermal energy, associated with the heat of an object.
  • Chemical energy, stored in the chemical bonds of molecules.
  • Electrical energy, associated with the movement of electrons.
  • Electromagnetic energy, associated with light waves (including radio waves, microwaves, x-rays, infrared waves).
  • Mass (or nuclear) energy, found in the nuclear structure of atoms.

The law of conservation of energy:

i) Energy cannot be created or destroyed - it is constant.
ii) It can only be changed from one form to another.

Look at the data booklet:

Kinetic energy is the mechanical energy a body has due to its movement.

Ek = mv2/2

Look at the data booklet:

Potential energy is the mechanical energy a body has due to its position above the earth.

ΔEp = mgΔh where Δh is the difference in height between two locations and g = 9.81 .

There are also other forms of potential energy due to for example a bodys position in an electric field.

The total mechanical energy: Et = Ek + Ep

This total energy is constant unless the energy is transformed into another form of energy which is not mechanical, such as heat.



An elastic collision is a collision where the momentum and energy is conserved.



Look at the data booklet:

Power: P = W / t   →   Power = work done per unit time    Unit: Watt (W) or J/s

P = W / t = F•Δs/t = F•v    where v is the average velocity.

When one is working with heat the formula changes to P = Q / t where Q is the heat.

ε = Wout / Win   →   Efficiency = useful work out / energy put in    Unit: %

2.10 - Uniform circular motion

The time period (T) in circular motion is the time it takes for one complete turn. Unit: s

The frequency (f) in circular motion is the number of complete turns per unit time. Unit: Hz or s-1

f = 1 / T and T = 1 / f

Look at the data booklet:

The angular velocity (ω) is the angle swept over per unit time.

ω = 2π / T since the angle for a complete turn is 2π

ω = 2π / T = 2π•f since f = 1 / T

Look at the data booklet: