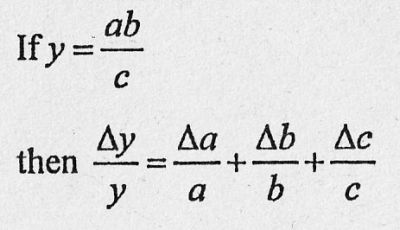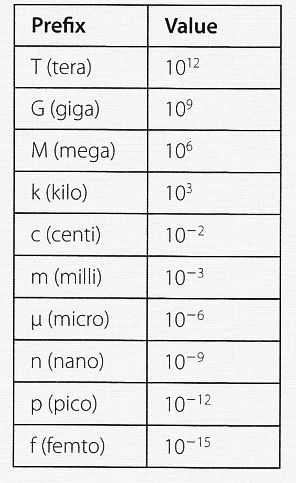
1.1 - Fundamental quantities - questions

1 - What do the prefixes nano, giga, micro, mega, kilo, pico and milli mean ?

2 - Convert 12.3 liters to m3 and write it in the standard form !

3 - Which are the fundamental units that all other derived units are made from ?

4 - What is the formula for density and what unit does it have ?

5 - What is the density of water and air ?

1.2 - Measurement - questions

6 - How do you estimate the error on a scale on for example a ruler ?

7 - Explain the difference between accuracy and precision and random error and systematic error.

1.3 - Collecting data - questions

8 - You measure 124.123456±0.0234546 . How should you report this value ?

9 - You measure 124.123456±2.34546 . What is the absolute and the relative error ?

9.1 - You measure two values a and b with the errors Δa and Δb .
Then you calculate a new quantity y = a + b.
What is the error on y ?

9.2 - You measure two values a and b with the errors Δa and Δb .
Then you calculate a new quantity y = a - b.
What is the error on y ?

9.3 - You measure three values a, b and c with the errors Δa , Δb and Δc .
Then you calculate a new quantity y = ab/c .
What is the error on y ?

9.4 - You measure a=1.1±0.1 b=2.1±0.3 b=3.1±0.3
calculate y = a + b - c

9.5 - You measure a=1.1±0.1 b=2.1±0.3 b=3.1±0.3
calculate y = ab/c

1.4 - Presenting data - questions

10 - Explain how you can estimate the error on the gradient of a straight line measurement !

1.5 - Vectors and scalars - questions

11 - What is a scalar and vector quantity ?



1.1 - Fundamental quantities

1 m3 = 1000 dm3 = 1000 liters

1 liter = 1/1000 m3 = 0.001 m3

12.3 liters = 0.0123 m3

Standard form means only one digit in front of the point → 12.3 liters = 0.0123 m3= 1.23 x 10-2 m3

Density: ρ = m / V where m is the mass and V is the volume. Unit: kg/m3

Density of water = 1.0 x 103 kg/m3

Density of air = 1.2 kg/m3

1.2 - Measurement

Take the difference between two marks and divide by two as an estimation of the uncertainty in a measurement. A ruler with a mm scale has then an uncertainty of ±0.5 mm.


Look at the picture above. It shows the result of someone shooting on a target.

The precision tells you how close the values you get when you repeat the same measurement again and again. The spread of the values of repeated measurements tells you how large the random error (or reproducibility error or statistical error) is. By calculating the average of all measurements you reduce this error.

The accuracy tells you how far off your measurements are from the true value. If you are very accurate all the measurements are centered around the true value. If the measurement is inaccurate there is something slightly wrong with all the measurements and the measurement has then a systematic error.

1.3 - Collecting data

If you measure 124.123456±0.0234546 you should report it as 124.12±0.02

If you measure 124.123456±2.34546 the absolute error is ±2
The relative error is 2.34546/124.123456 = 0.0189 i.e. the relative error (or the percentage error) is 2% .

If you measure two values a and b with the errors Δa and Δb and you calculate a new quantity y = a + b.
Then you find the error on y in the data booklet:

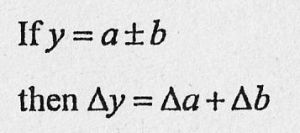
If you measure two values a and b with the errors Δa and Δb and you calculate a new quantity y = a - b.
Then you find the error on y in the data booklet:

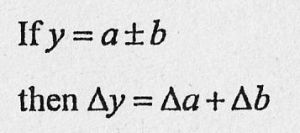
If you measure three values a, b and c with the errors Δa , Δb and Δc and you calculate a new quantity y = ab/c .
Then you find the error on y in the data booklet:

a=1.1±0.1 b=2.1±0.3 b=3.1±0.3
y = a + b - c = 1.1 + 2.1 - 3.1 = 0.1
Δy = Δa + Δb + Δc = 0.1 + 0.3 + 0.3 = 0.7

So y = 0.1±0.7

a=1.1±0.1 b=2.1±0.3 b=3.1±0.3
y = ab/c = 1.1 x 2.1 / 3.1 = 0.75
Δy = y(Δa/a + Δb/b + Δc/c) = 0.75(0.1/1.1 + 0.3/2.1 + 0.3/3.1) = 0.25

So y = 0.75±0.25

1.4 - Presenting data


1.5 - Vectors and scalars

Scalar quantity: A quantity with magnitude only.

Vector quantity: A quantity with magnitude and direction.