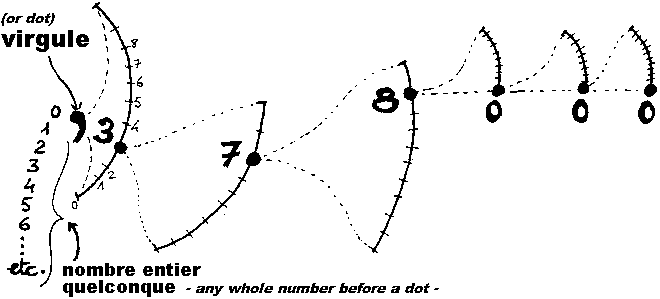
| I
accueil |
E
sommaire Mathématique |
avant
: E
les infinis schizophrènes de Cantor |
suite
: F
comment voyager d'un nombre à l'autre |
| accès direct à tous les autres textes de la section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
|
On ne démontrera pas que Cantor fait une erreur de raisonnement logique quand il s'approche de l'infini ou lorsqu'il prétend l'atteindre. On essaiera de démontrer que c'est au départ même qu'il prend un mauvais chemin. Cantor
nous demande de commencer par ranger en ligne tous les nombres irrationnels.
Or, tous les nombres irrationnels ne peuvent tout simplement pas se mettre
tous en même temps, sur une même ligne.
|
Pour le démontrer, il faut
revenir à la source, c'est-à-dire à la façon
dont les nombres sont produits selon la théorie des ensembles.
Commençons par les nombres
entiers.
|
Dans la théorie des ensembles, la méthode la plus usuelle pour produire les nombres entiers est de commencer par faire un constat : on dit qu'aucune chose ne peut être le contraire d'elle-même. Par exemple, qu'aucune chose ne peut être à la fois positive et négative, à la fois ici et pas ici, etc. Ce constat réalisé, on fait un paquet de toutes les choses qui sont contradictoires avec elles-mêmes : ce paquet ne contient rien. On l'appelle alors "l'ensemble vide". Puis on dit que l'ensemble vide cela correspond au chiffre "zéro". Le chiffre zéro, cela sert à se souvenir que l'on a fait un paquet qui s'appelle l'ensemble vide. C'est une étiquette qui n'est pas mise sur l'ensemble vide lui-même. L'étiquette de l'ensemble vide, c'est-à-dire son nom c'est : "l'ensemble vide". Zéro, c'est l'étiquette qui correspond à l'opération même de mise en paquet, de désignation de l'ensemble vide, de reconnaissance de son existence. C'est à cet acte que zéro sert d'étiquette, c'est-à-dire de nom. Zéro, c'est donc le constat de ce que l'on a, quand on a rien. On a donc un ensemble vide. "Un" ensemble vide ? Mais ce n'est pas rien cela ! C'est "une" chose. Mettons tout de suite une étiquette à ce constat que l'on vient de faire, qu'il y a "un" ensemble vide. Disons que ce constat sera le chiffre "1". On a donc fait le constat d'un ensemble vide et le constat d'un ensemble qui contient 1 chose (l'ensemble vide précisément), cela fait donc 2 choses. Vite, une étiquette pour nous rappeler de ce nouveau constat : le chiffre "2". Cela fait donc 3 choses maintenant : le chiffre "3", etc. bien sûr, et jusqu'à l'infini. |
Quand on génère ainsi
les nombres, à partir de la mise en ensemble des choses qui sont
le contraire d'elles-mêmes, on remarque deux faits.
- d'une part, on ne trouve jamais dans les nombres que l'on produit ainsi,
quelque chose qui ressemble de près ou de loin à un nombre
décimal, fractionnaire, ou irrationnel. On tombe toujours pile sur
des entiers, jamais entre deux.
- d'autre part, on s'aperçoit que l'on ne peut pas faire le constat
du vide d'éléments dans un ensemble, sans constater en même
temps qu'il existe "1" tel ensemble qui ne contient rien, donc qu'il y
a du rien et du 1, donc 2 choses, donc du rien du 1 et du 2, donc 3 choses,
etc. Faire ainsi 0, 1, 2, 3,
4, etc à l'infini, ce n'est donc pas avancer progressivement comme
sur une droite, par petits sauts répétés se produisant
les uns après les autres et faisant à chaque fois sur cette
droite une encoche séparée de la précédente
et de la suivante. C'est au contraire faire défiler d'un seul coup
tous les nombres jusqu'à l'infini, alors même qu'on en est
encore à faire le 0.
Tous
les nombres entiers sont donc contenus dans le zéro, ramassés
dans le zéro, même l'infini.
Bien sûr, après coup,
c'est-à-dire après les avoir générés,
rien ne nous empêche de ranger tous les nombres entiers positifs
sur une droite qui part de 0 et va jusqu'à l'infini. Mais c'est
alors un rangement, un étalement. Cela n'a rien à voir avec
la dynamique de création des nombres entiers.
Cela n'a rien à voir avec
le fait qu'ils existent, qu'on peut les produire.
|
Maintenant que nous avons les nombres entiers, passons aux nombres décimaux, tels que 0,1 ou 0,23489421. Tous les nombres entiers étant ramassés sur 0, il n'y a pas de distance entre le 0 et le 1, donc pas de trajet possible entre le 0 et 1. Aucun trajet que l'on pourrait graduer en mettant l'étiquette d'un nombre décimal à tous les intervalles rencontrés. Si l'on veut graduer quelque chose sans pouvoir circuler sur ce quelque chose en faisant des marques le long de ce trajet, le seul moyen que l'on ait consiste à simplement déformer cette chose, et à garder souvenir de l'intensité de cette déformation. C'est ainsi que l'on va générer les nombres décimaux : en graduant l'intensité d'une déformation, de telle sorte que l'absence complète de déformation sera notée 0, et que la déformation maximum possible sera notée 1. |
Comment nous y prenons-nous ?
Prenons un nombre décimal
quelconque, par exemple 0,340238911352. On constate, rien qu'en l'écrivant,
plusieurs faits incontournables :
1/
D'abord, on met une virgule. C'est-à-dire que l'on met une étiquette
d'un type spécial, qui sert à nous souvenir que ce qu'il
y a à gauche et à droite de ce signe, ne doivent pas être
mélangés.
2/
Ensuite, derrière la virgule on met plusieurs chiffres qui
sont autant d'étiquettes à des choses dont on veut se souvenir.
Dans ce cas, on a employé 12 chiffres après la virgule. Si
l'on a employé 12 chiffres, c'est qu'on en avait besoin. Si l'on
avait pu en utiliser moins, on l'aurait fait. On sait par contre, qu'on
peut en rajouter autant que l'on veut après ces 12 premiers. Cela
ne changera pas le nombre, à condition seulement que l'on ne rajoute
que des chiffres 0.
3/
L'ordre des chiffres, a par ailleurs son importance : le nombre 0,129 n'est
pas du tout le même que le nombre 0,912. Il y a donc aussi
quelque chose dont on veut se souvenir qui est contenu dans l'ordre avec
lequel on range les chiffres derrière la virgule.
4/
Dernier point important : on n'emploie que 10 étiquettes différentes
qui suffisent à créer et désigner tous les nombres
décimaux : les étiquettes 0, 1, 2, 3, 4, 5, 6, 7, 8 et 9.
Ce dont on veut garder la trace à chaque chiffre après la
virgule, est donc quelque chose qui ne peut prendre que 10 valeurs régulièrement
graduées. On peut noter en passant, que l'on aurait pu s'y prendre
autrement : au lieu d'employer les 10 premiers nombres entiers, on aurait
pu utiliser des lettres de l'alphabet, ou même n'importe quel petit
dessin. Le fait qu'on emploie les 10 premiers nombres entiers pour nommer
les chiffres décimaux, n'a rien à voir avec le fait que ce
sont des nombres. C'est seulement qu'on se souvient plus facilement de
l'ordre dans lequel ils sont rangés, que de l'ordre dans lequel
sont rangés par exemple 1 étoile, 1 trèfle à
quatre feuilles, et 1 as de pique.
On n'est pas obligés non
plus d'employer 10 graduations. Ce nombre n'est valable que pour les nombres
que l'on appelle "de base 10". On peut aussi employer des nombres "de base
16" ou plus. En fait, plus le nombre d'étiquettes est grand, moins
on a besoin d'en mettre derrière la virgule, car la gamme de graduations
couverte par chaque étiquette est d'autant plus fine. L'informatique
utilise couramment cette propriété en prenant toutes les
lettres de l'alphabet et même tous les autres signes du clavier,
à la place de nombres. Cela permet à chaque nombre, formé
à partir de choix successifs dans cette multitude de signes, d'être
composé de moins "d'étiquettes après la virgule" que
s'ils étaient formés à partir de choix successifs
entre les 10 premiers nombres entiers, ce qui permet ainsi de tenir moins
de place dans la mémoire de l'ordinateur. Ainsi un nombre peut être
conservé par exemple sous la forme : 4#DF
|
Maintenant que nous avons énuméré tous les types de traces dont nous cherchons à nous souvenir quand nous nommons un nombre décimal, décrivons pas à pas comment nous procédons pour produire un tel nombre. On prend d'abord un nombre entier, de 0 à l'infini positif ou de 0 à l'infini négatif, et on le laisse intact, sans déformation. Puis à sa suite on place une virgule, qui signale qu'à partir de là on va commencer à faire quelque chose d'une autre nature que le nombre entier déjà placé. Quelque chose qu'on n'a pas pu ramener dans ce nombre, qu'on n'a pas pu désigner en même temps que lui. Après la virgule, ce que l'on va faire c'est énumérer l'une après l'autre des intensités de déformation. Déformation de quoi ? De tout ce que vous voudrez, car on ne va pas enregistrer la matérialité de ces déformations, seulement noter leur intensité. On fait d'abord une première déformation dont l'intensité sera repérée par une 1ère étiquette mise après la virgule. Dans notre système de base 10, on a 10 valeurs d'intensité à notre disposition. Et de deux choses l'une : ou bien le nombre que l'on cherche à indiquer correspond précisément à l'une de ces 10 valeurs possibles de déformation, ou bien il n'y correspond pas. Il ne peut pas être « entre » deux valeurs, puisque les valeurs que nous envisageons ne correspondent pas à des coordonnées sur une courbe se traçant dans l'espace, mais à des intensités de déformation : comme il n'y a pas d'espace entre deux valeurs, il ne peut y avoir de notion de « entre » ces deux valeurs qui ne sont écartées d'aucune distance l'une de l'autre. Si notre nombre n'est pas exactement obtenu après cette première déformation, on va garder comme souvenir l'étiquette qui correspond à l'intensité de la dernière déformation trouvée avant que l'on s'aperçoive qu'on a raté le nombre. Ce n'est pas "la plus proche" du nombre cherché puisque, à nouveau, il n'y a pas de distance quelconque à ce nombre : c'est "la dernière" avant le constat de son ratage. Donc, une première déformation,
sautant par crans d'intensité rigides de 0 à 9, n'a pas suffi
pour obtenir le nombre. Alors on recommence avec une 2ème déformation,
dont on garde le souvenir de la même façon en désignant
l'intensité mesurée quand on a raté le nombre.
Etc, jusqu'à ce que l'on obtienne le nombre exact que l'on cherche.
|
La question
revient donc maintenant : tous ces nombres fractionnaires et irrationnels
que l'on peut produire de cette façon, peut-on les mettre alignés
tous ensemble sur une même droite, et de préférence
sur une même droite que les nombres entiers ?
Cette
fois, la réponse est non ! Catégoriquement non !
Car si l'on veut garder toutes
les informations qui nous ont été utiles pour obtenir un
nombre décimal, on doit garder la trace de toutes ces déformations
successives, et de leur ordre de survenue.
Si l'on veut garder toutes ces informations
sous forme "d'espace", c'est-à-dire de graphique, le moins que l'on
puisse faire, c'est d'étaler cette succession de déformations
les unes à côté des autres, sans en changer ni l'ordre,
ni le nombre, ni la valeur de l'intensité constatée à
chaque ratage. Perdre une seule
de ces informations, c'est perdre ce qui distingue un nombre d'un autre,
c'est confondre abusivement deux nombres différents, c'est perdre
le nombre que l'on voulait figurer dans un espace en le mélangeant
à d'autres.
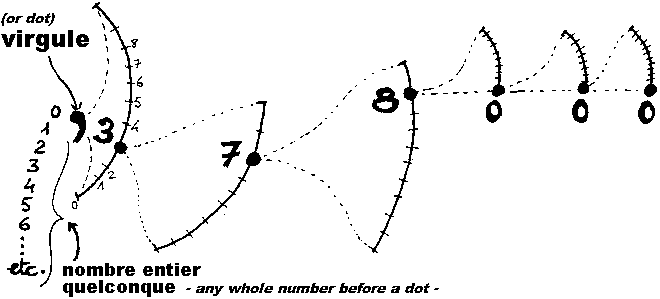
|
Si l'on dessine un schéma qui conserve toutes ces informations, on voit clairement qu'un nombre décimal requière, pour être représenté, un espace à 2 dimensions au minimum : une surface donc, non pas une droite qui n'a qu'une dimension. |
Si par commodité on accepte de perdre des informations sur les nombres afin de les placer sur une même droite, on doit bien entendu s'abstenir d'utiliser ce mode de rangement qui les massacre, pour faire des démonstrations sur leurs propriétés. C'est pourtant ce que nous demande Cantor quand il commence par nous demander : "mettez dans une même colonne tous les nombres irrationnels". Si l'on prolonge jusqu'à l'infini un raisonnement qui a commencé par massacrer les nombres en leur faisant perdre plus de la moitié de leurs propriétés, il ne faut pas s'étonner si l'on obtient des monstres en arrivant à l'infini. Ni non plus s'en inquiéter.
Même les nombres entiers ne
peuvent être valablement représentés tous ensemble
par une ligne droite. Car il y a plus d'information dans la suite infinie
des nombres entiers, qu'il n'y en a dans la suite infinie des points sur
une droite. Cette information est que les nombres entiers sont à
la fois tous confondus avec zéro, et tous décalés
de +1 les uns des autres. Les points d'une droite sont "seulement" différenciés
par un décalage entre eux. Ils ne sont pas "en plus" rassemblés
en un même point.
L'information contenue dans l'ensemble
des nombres entiers n'étant pas du même type que celle contenue
dans l'ensemble des points d'une droite, on ne peut par conséquent
prétendre utiliser les propriétés de l'une, pour en
déduire les propriétés de l'autre.
| I
accueil |
E
Math |
G
haut |
suite : F comment voyager d'un nombre à l'autre |
|