accueil

sommaire Art

avant :    mais à quoi sert donc une poivrière ?

suite :    un exemple de complexité en évolution

le stade 0 de la complexité

         Ce que nous désignons comme le premier stade de la complexité, correspond à l'existence de points seulement séparés les uns des autres. Nous avons des points écartés les uns des autres, et puis c'est tout.
         Ce point parmi d'autres points, peut être un atome parmi d'autres atomes, il peut aussi bien être un être humain parmi d'autres humains, ou encore être un tracé parmi d'autres tracés. Tout ce que l'on demande à la situation pour correspondre à ce stade, c'est qu'elle traite de faits que l'on peut résumer chacun par une position, et que ces positions soient écartées les unes des autres, sans que l'une ou l'autre n'ait une position spécialement remarquable qui la distingue des autres. Un ensemble de points répond bien sûr à cette situation, c'est pourquoi nous appellerons ce stade, "le stade des points séparés". Nous l'appellerons aussi le stade de dimension 0, nous souvenant que les mathématiciens disent que les points sont des figures sans dimension, ou de dimension nulle.
 
 

le stade des points séparés

         Tout à fait contemporaine cette fois, on peut citer cette toile du peintre d'origine allemande A.R. Penk, qui date de 1971, et qu'il a intitulée "Emplacement". Sur la partie gauche de la toile, se trouve tout un amas de points dont on ne peut guère dire plus, qu'ils sont dispersés les uns à côté des autres.
 

         Les fleurs blanches du premier plan forment, dans chaque arbuste, comme un bouquet de points régulièrement étalés. La même chose vaut pour les grappes de feuillages qui sortent de chaque arbuste du second plan, ou pour les étoiles de la toge de Saint Mathieu. À plus grande échelle cela vaut pour les bouquets et pour les arbustes eux-mêmes, et pour les moutons. En second plan, les pierres et les touffes d'herbe, également se répandent de façon dispersée et assez régulière.
         Bien sûr, l'organisation de cette mosaïque combine cet effet de points avec d'autres effets, notamment des effets d'alignements et de hiérarchies entre végétaux de diverses tailles, mais l'on a déjà prévenu que nous allions avoir à démêler plusieurs stades de complexité entremêlés, ce que nous ne pourrons faire que plus tard.
         Cet exemple avait seulement pour but d'exposer comment par "points", il ne faut pas forcément entendre de gros tracés bien ronds, mais des éléments de formes identiques et dont les positions sont régulièrement étalées. Comme les formes sont identiques, on se concentre sur la position de ces formes et non sur leurs particularités, et comme ces positions sont équivalentes, on sait que l'on a affaire à ce stade qui traite de positions séparées et équivalentes entre elles.
 

fleurs ayant le statut de points équivalents entre eux	feuillages ayant le statut de points équivalents entre eux	cailloux ayant le statut de points équivalents entre eux	touffes d'herbe ayant le statut de points équivalents entre eux

 
 
 
 

le stade 1 de la complexité

         Dans un sens, on peut dire que le premier stade, celui du point, ne comprend rien. Il ne comprend rien puisqu'il comprend seulement des positions géométriques. Le second stade ne comprend d'ailleurs rien de plus,  puisqu'il ne comprend lui aussi que des points, et absolument rien d'autre. Pour comprendre ce qui peut faire que la situation soit malgré tout plus complexe, il suffit de réfléchir à ce qui peut arriver à des points pour que leur situation soit plus compliquée, sans pour autant ne contenir rien d'autre qu'eux-mêmes. La seule complication qui peut arriver à des points séparés, c'est que ces points se classent entre eux. C'est-à-dire qu'ils cessent d'être des points équivalents et interchangeables, pour que l'on puisse maintenant les distinguer les uns des autres. Si par exemple trois points se trouvent sur une même ligne, l'un se distinguera des autres comme étant au milieu, et les deux autres se distingueront de lui comme étant en extrémité de leur petit groupe. Ce ne sont toujours que des positions, mais ces positions ne sont plus équivalentes, on peut les distinguer.
         Voyez que par classement on n'entend pas spécialement que les points se rangent dans un ordre régulier, mais on entend seulement que leurs positions - puisqu'ils ne sont que cela - puissent se remarquer de façon particulière, qu'elles se distinguent les unes des autres et ne soient pas quelconques ou équivalentes. Que le classement soit "en bon ordre" ou "sans ordre précis", un classement distingue la position des éléments qui le constituent : on peut toujours dire que l'un est devant tel autre, et qu'il est derrière tel autre.
         Le dessin de points séparés permettait de résumer la notion de positions. De la même façon, nous pouvons utiliser un graphisme pour résumer la notion de classement. Comme on l'a vu, trois points alignés pourraient servir à cela, mais rien ne garantit que cet alignement n'est pas fortuit et qu'il se conservera quand les points viendront à bouger. Aussi, nous utiliserons plus volontiers un trait droit, puisqu'un trait possède nécessairement un centre et deux extrémités, donc trois endroits clairement différents les uns des autres.
         Un trait droit résume de façon synthétique :
         - le fait qu'il y a des endroits aux positions distinctes (ce qui correspond au stade du point) ;
         - et le fait que ces positions ne sont pas seulement équivalentes ou interchangeables, mais qu'en plus d'êtres distinctes elles sont aussi différentes l'une de l'autre (ce qui correspond au stade du classement).
         Qui plus est, toutes ces propriétés restent parfaitement lisibles lorsque le trait fait un mouvement dans l'espace.
 
   

le stade du classement de plusieurs points

         Deux ou trois personnes pouvaient être équivalentes à trois points isolés, dès lors qu'on ne faisait que constater qu'elles occupaient des positions différentes.
         Si l'on note maintenant qu'elles sont peut-être de sexe différent, ou de taille différente, ou de race différente, alors on ne les considère plus seulement formant un groupe de points seulement séparés, mais on considère le classement qu'elles forment en se distinguant les unes des autres par le sexe, la taille ou la race.
         Ce second stade de la complexité, nous lui donnerons la dimension "1". "0" pour les points, "1" pour les traits droits, on voit que cette numérotation continue le chiffrage habituel des mathématiciens qui attribuent la dimension 0 à un point et la dimension 1 à une droite.

         Il est important de remarquer que pour faire un classement de points, il faut d'abord disposer de points séparés, et il faut ensuite que ces points ne disparaissent pas en s'amalgamant l'un sur l'autre. Toujours d'ailleurs nous retrouverons cette règle simple : tout stade de complexité contient en lui-même tous les stades successifs qui l'ont précédé, et ces stades successifs ne disparaissent pas en se fondant dans le stade nouveau, mais ils restent vivants et actifs en lui. De là provient d'ailleurs le caractère contradictoire que l'on a souligné d'emblée pour la société humaine : dès lors que l'on se perçoit comme un classement de points, on doit aussi considérer que l'on est en même temps et indissociablement un ensemble de points non classés, c'est-à-dire que l'on doit se ressentir à la fois comme une chose et pas comme cette chose.
         On peut aussi faire une autre remarque liée à la précédente : si les stades antérieurs subsistent, ils doivent être capables de ne pas se défaire. Pour des points seulement séparés, cela signifie que, quoi qu'il advienne, ils doivent rester écartés et ne pas s'agglomérer l'un à l'autre. Pour des points classés, cela signifie que leur classement doit tenir. Si ce classement est permis par un alignement, les points doivent rester alignés, si c'est une différence de taille ou de vitesse qui les distingue, cette différence doit toujours subsister, etc. La question se pose donc : comment ces propriétés peuvent-elles se conserver sans se fondre dans les propriétés du niveau supérieur qui les absorbe ? Pour  l'instant, nous ne répondons pas à la question, nous la laissons en suspens, mais nous y reviendrons à l'occasion du quatrième stade de la complexité . . . car précisément le quatrième stade est celui qui nous apportera la réponse.

         Pour illustrer le second stade, nous pouvons donner des exemples tirés de l'histoire de l'art où l'effet de classement apparaît clairement.

Certainement les alignements de mégalithes, tels ceux de Carnac en Bretagne (France), sont spécialement caractéristiques de cet effet. Chaque pierre dressée figure un classement, avec trois positions bien différenciées l'une de l'autre : l'extrémité qui touche le sol, la partie médiane, et l'extrémité pointée en l'air. Ces classements à leur tour se mettent en longues rangées, et parfois plusieurs rangées se tracent l'une à côté de l'autre.

 

si l'on néglige leur forme, les pierres sont perçues comme des points équivalents interchangeables	si l'on prête attention à leur forme, les pierres se différencient l'une de l'autre et sont perçues comme des points classés entre eux de façon repérable

 
         Un autre exemple de classement nous est donné par les gravures sur roches en plein air de la "vallée des merveilles" (Alpes Maritimes, France). Elles correspondent à un stade de complexité de la société seulement quelques pas plus tardifs que celui des alignements de mégalithes. Nous donnons un exemple de ces gravures qui datent de 1 800 à 1 500 environ avant notre ère, et qui représentent des têtes de bucanes figurant un troupeau.
 

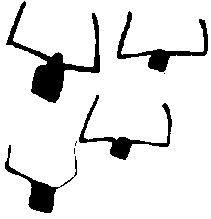
        Ce sont des classements faits de traits presque droits qui sont utilisés ici. Ces classements sont eux-même classés de deux façons différentes. Certains classements de classements sont bouclés sur eux-mêmes : ce sont les traits qui forment les quatre côtés de la tête en silhouette de chaque animal. Et les autres sont des classements de classements que l'on peut appeler par différence des classements ouverts : ce sont les cornes des animaux, chacune faite de deux traits/classements séparés l'un de l'autre par un coude. On distingue bien l'un de l'autre les deux classements qui forment chaque corne, du fait que l'un est proche de la tête et que l'autre en est éloigné. De même, les traits/classements qui cernent chaque tête sont bien classés entre eux puisqu'ils ont des situations différentes : l'un prolonge les cornes par ses deux bouts, un autre ne touche aucune corne, et les deux autres ne touchent une corne que par un bout. On verra le moment venu que cette juxtaposition de deux types de classements, l'un fermé sur lui-même, l'autre ouvert en extrémité, correspond à un effet bien précis et récurrent dans l'évolution de la complexité.
 

le museau : classement fermé sur lui-même de 4 traits de contour, chacun étant lui même un classement	une corne : classement de 2 traits ouvert à son extrémité, chacun de ces 2 traits classés étant lui-même un classement

 
 

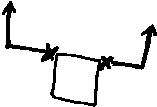         Si l'on jette à nouveau un regard sur la toile de Penk, on s'aperçoit bien entendu que la partie droite est remplie de traits/classements qui eux-mêmes ne sont pas classés entre eux mais sont traités comme les points séparés de la partie gauche. Le bonhomme quant à lui, est entièrement construit à l'aide de traits/classements impliqués dans des situations variées qu'il est encore trop tôt pour analyser.
         L'empreinte (de main ?) qui occupe le centre des points de gauche, effectue une transition progressive remarquable entre ses quatre points horizontaux du haut non classés entre eux, et trois trapèzes ou rectangles alignés verticalement qui, du fait de leur forme différente, sont par contre clairement classés entre eux. Le bonhomme central présente d'ailleurs la même particularité : la moitié gauche et la moitié droite sont équivalentes, alors que son haut se différencie clairement de son bas.
 

 

 le stade 2 de la complexité

         D'abord nous avions des points, c'est-à-dire des riens, mais des riens que nous pouvions localiser. C'était déjà mieux que rien. Puis ces riens localisés, maintenant nous savons les différencier. Les uns sont par exemple les centres, et les autres sont les extrémités d'une file de riens. C'est maintenant beaucoup mieux que rien, et c'est déjà la moitié de ce qu'il faut pour construire une complexité.
         Étant toujours supposé que des classements peuvent tenir sans se défaire - on verra plus loin comment -, quelle complexité plus grande pouvons nous cette fois envisager ? Pour respecter la règle que nous avons utilisée jusqu'ici, ce nouveau stade ne doit introduire aucun élément nouveau que nous ne possédions déjà, et il doit seulement se baser sur un arrangement particulier des éléments qui sont déjà là.
         Si nous prenons plusieurs classements quelconques au lieu d'un seul classement, avons nous une propriété nouvelle ? Nous avons plusieurs classements localisés en des endroits distincts, ce qui n'est pas nouveau mais nous ramène seulement un pas en arrière en faisant fonctionner ces classements comme autant de points séparés.
         Si nous classons ces classements entre eux de quelque façon, par exemple en les distinguant pas la couleur, nous n'obtenons pas non plus une propriété nouvelle, car nous nous contentons de reproduire à une échelle supérieure la propriété de classement que chacun déjà possède.
         Alors quoi, n'y a-t'il rien à tenter ? Si : il reste la possibilité de croiser les classements.
         Croiser des classements, c'est établir deux classements simultanés des mêmes points, ou si l'on veut, classer les mêmes points dans deux directions à la fois, ou de deux manières différentes à la fois.
         La façon la plus synthétique d'exprimer que le classement entre plusieurs points s'effectue en même temps selon deux classements distincts, est certainement de courber le trait que forme un classement. Un segment est, comme on l'a vu, l'équivalent du classement de trois points, puisque l'un se définit par rapport aux deux autres et s'en distingue comme étant leur milieu. Si dans le même temps ce segment se courbe, une autre relation différente mais absolument simultanée va s'établir entre les points : l'un sera nécessairement plus près de nous qu'un autre et peut-être que les deux autres, et leur éloignement respectif de nous sera alors un autre moyen de les différencier les uns des autres. Même si la courbe se déplace dans l'espace et que l'ordre de cet éloignement respectif se modifie, il restera toujours une différence d'éloignement qui différenciera entre eux les trois points. Le classement se modifiera, mais il restera un classement de même type, et différenciant entre eux les mêmes points, ce qui est tout ce que nous lui demandons.
         Pour définir ce nouveau stade de la complexité, nous dirons qu'il consiste à organiser deux classements différents et simultanés d'un même ensemble de points. Pour cette raison nous l'appellerons "le stade de l'organisation" et nous lui donnerons la dimension "2", valeur qui rappelle la dimension "2" que les mathématiciens utilisent pour une surface obtenue par le croisement de deux droites portant chacune la dimension "1" d'un classement. 
 

le stade de l'organisation   de deux classements simultanés de plusieurs points (ses 2 expressions possibles)

         Cette fois encore, pour aider à comprendre ce que ce stade implique comme jeu spécifique de formes, nous allons donner quelques exemples tirés de l'histoire de l'art.

         Le déchiffrage du langage des formes que nous proposons n'est pas spécialement adapté à l'art préhistorique, mais du fait que cet art correspond à un avancement encore modéré de la complexité de la société, il nous est précieux pour présenter les notions utiles sous forme d'abord simple. Les arts des périodes ultérieures utilisent les mêmes effets, mais leur combinaison sur plusieurs niveaux rend leur lecture moins immédiate.
         Voici donc un exemple d'art préhistorique qui fait un usage immodéré du trait courbe dont on a dit qu'il représente un double classement simultané. C'est l'une des dalles gravée du dolmen de Gavrinis en Bretagne (France), qui date de 4 à 5 000 ans environ avant J.C.. Ici, le trait courbe est presque le seul motif utilisé : ils s'emboîtent les uns dans les autres, il en pousse au sommet de certains, ils s'alignent dans un sens et dans l'autre sens perpendiculaire, il y en a des grands bien rangés au milieu et des petits qui vagabondent sur les bords de la dalle.
 

     Pour donner un autre exemple truffé de classements et d'organisations, tout en changeant complètement de lieu et d'époque, voici la pagode du temple d'Hôryû-ji (préfecture de Nara) au Japon. Ce temple date de 607 après J.C., mais a été reconstruit entre 670 et 714 après qu'un incendie l'ait détruit.
     Chaque bord de toit forme le classement de deux extrémités et d'un centre. Ces bords s'arrondissent en leurs extrémités, ce qui les différencie d'une manière supplémentaire de la zone centrale qui reste droite, et qui transforme donc chaque bord en organisation. À leur tour, ces organisations se différencient l'une de l'autre en partant dans des directions horizontales croisées qui font le tour de chaque étage, et se différencient d'une seconde manière en se répartissant sur des étages successifs. Les bords de toit se différencient donc les uns des autres en se trouvant plus ou moins sur le devant ou sur le côté, et en même temps plus ou moins en bas ou plus ou moins en haut de la pagode.
     Ce type de classement simultané selon plusieurs directions est une autre façon de réaliser une organisation. Cette pagode nous propose donc des organisations de rangements obtenus par effet de courbure, qui elles-mêmes s'organisent en rangements qui se croisent selon des directions horizontales et verticales.
     On profite de cette image pour attirer l'attention sur l'empilement de courbes / organisations qui forme la crête verticale qui surmonte la pagode.
 

le stade 3 de la complexité

         Très vite, et sans avoir affronté des affres de difficultés, nous en sommes donc déjà rendus au quatrième et dernier stade de la complexité. Au seuil de ce stade :
          -  nous disposons de l'organisation de deux classements simultanés ;
          -  chacun correspond au classement des mêmes points ;
          -  et ces points classés restent en même temps des points séparés.
         Ainsi nous disposons donc des trois stades de complexité antérieurs, enchâssés l'un dans l'autre, et toujours aussi vivants l'un que l'autre. Et nous devinons que cette fois encore nous n'aurons rien de nouveau à ajouter pour obtenir la propriété nouvelle qui signalera ce nouveau stade.

         Aux points séparés, d'abord différenciés l'un de l'autre d'une certaine façon, puis maintenant différenciés simultanément d'une autre façon, nous n'aurons en effet rien à ajouter, puisque la propriété nouvelle viendra cette fois encore d'une configuration particulière que saura prendre le stade précédent. Cette propriété nouvelle sera que l'organisation des classements trouvera maintenant le moyen de ne plus jamais se défaire.
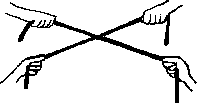
         Si vous prenez une corde tendue entre vos mains, vous avez l'équivalent d'un classement : deux bouts et un milieu. Si vous demandez à une autre personne de prendre une autre corde tendue entre ses mains et de l'affronter à la votre, de pousser votre corde avec la sienne, vous pourrez alors avoir l'équivalent d'une organisation de deux classements : en poussant sur l'une des cordes vous déformez l'autre aussitôt, et les deux réagissent ensemble. Mais cela n'est pas vrai dans toutes les configurations, vous pouvez toujours trouver des positions où les deux cordes glissent l'une sur l'autre sans s'entraîner mutuellement, et vous pouvez aussi tirer en arrière l'une des cordes pour la détacher de l'autre.
         Bref, l'organisation de vos deux cordes présente des faiblesses selon certains angles, et peut alors se défaire. Pour que vos cordes bougent certainement l'une en même temps que l'autre, et cela de façon constamment liée, l'astuce consiste très simplement et très précisément à les lier, c'est-à-dire à les nouer. Un noeud est-il quelque chose de nouveau pour les cordes ? Non, la corde n'est ni plus longue ni  plus grosse après qu'on l'ait nouée, elle possède seulement une propriété géométrique particulière qui ne représente absolument rien en termes matériels.
 

2 organisations détachables	et 2 organisations nouées

le stade du nouage   de l'organisation de deux classements simultanés de plusieurs points

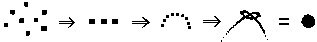         Ce quatrième stade de la complexité, tout normalement aussi nous lui donnons le nom de "stade du noeud", et nous lui donnons la dimension "3", qui n'a pas d'équivalent évident cette fois avec les dimensions que les mathématiciens assignent à l'espace qu'on dit à 3 dimensions.
         Pour illustrer ce stade du noeud, nous ne pouvons pas donner maintenant des exemples tirés de l'histoire de l'art. Nous ne pouvons pas le faire, car le stade du noeud présente une particularité qui tranche avec celles des trois stades précédents. En effet, chacun de ces premiers stades s'éprouve dans l'espace : c'est une relation géométrique visible dans l'espace que celle où les points sont séparés ou agglomérés, c'est aussi une relation que l'on peut voir dans l'espace que celle où les points sont reliés entre eux dans une ou dans plusieurs directions. Mais un noeud, sa propriété essentielle, c'est de tenir bon, c'est-à-dire de durer. La qualité de noeud est donc fondamentalement quelque chose qui s'éprouve dans le temps, dont la fonction première est de permettre à ce qui s'est d'abord construit dans l'espace, de maintenant durer dans le temps.
         À cause de cette particularité du noeud il n'y a donc pas de figure spatiale représentative de cette propriété, et c'est toujours par le fonctionnement et la combinaison de propriétés spatiales simultanées que nous pouvons éprouver dans l'art, l'effet de noeud.
         Ces réflexions nous rappellent opinément que l'univers lui-même fonctionne avec trois dimensions d'espace et une dimension de temps. Au choix, on peut y voir un hasard, ou une signification profonde. Je penche pour ma part vers la signification profonde, et je suis persuadé de ce que si, dans notre univers peuvent se développer des complexités comprenant trois dimensions progressives qui s'éprouvent dans l'espace, puis une dernière dimension qui s'éprouve dans le temps, c'est que l'univers lui-même fonctionne et se complexifie à tous ses niveaux et à toutes ses époques, en répétant un processus analogue à celui que nous essayons ici de mettre à jour.
         L'irréversibilité du temps qui passe est d'ailleurs le meilleur exemple que l'on peut donner d'une situation nouée, puisque l'irréversibilité signifie que tout retour en arrière est impossible.

accueil

Art

haut

suite :     un exemple de complexité en évolution

auteur