la question des dimensions
 
         C'est précisément maintenant que nous butons sur le problème de dimension que nous avions annoncé  [revoir  E cette annonce]. Car pour pouvoir décrire la reproduction d'une protéine de cette façon, il faut réaliser dans nos têtes cette nouvelle révolution copernicienne.
         En effet, pour expliquer de cette façon la reproduction des protéines, on a supposé que  les parties codantes de l'ADN forment des figures magnétiques en creux dans l'espace, dans lesquelles l'ARN se précipite. Or dans la réalité, sauf au moment de la division cellulaire, l'ADN ne forme pas du tout une structure cohérente et stable dans l'espace. Il est sous forme de chromatide déroulée, lâche, informe, flageolante. Les parties codantes ne sont pas rassemblées en figures continues comme on l'a suggéré, mais sont dispersées aléatoirement au grès du ruban d'ADN.
 

 
 
 

Ce que l'on voit contredit donc toute l'hypothèse que l'on a proposée !              Pour dépasser ce conflit apparent entre notre hypothèse et la réalité perçue, il va falloir apprendre à penser de la même façon que fonctionne l'univers. Et l'on va suggérer que, pour l'univers, ce qui est séparé dans l'espace, n'est pas forcément réellement séparé.           Ce qu'il va falloir comprendre, c'est comment, bien qu'apparemment séparés dans l'espace quand le chromosome est déroulé, les parties codantes d'une même protéine fonctionnent exactement comme si elles étaient réunies dans une figure à trois dimensions dans l'espace, et pourquoi cela ne fait pas de différence pour la fabrication des protéines par la cellule, que le chromosome soit sous sa forme de bâtonnet condensé réellement cohérent en trois dimensions, ou sous sa forme de chromatide déroulée dans l'espace sans forme apparemment visible.

 
 
         On ne peut proposer tout de suite l'explication complète de ce mystère apparent, mais essayons néanmoins de donner un aperçu de la façon dont le problème se pose.
         Imaginons par exemple que l'on dessine un bonhomme sur une feuille de papier en déplaçant le crayon toujours à la même vitesse, et que vous assistiez à son dessin.
         La feuille de papier a deux dimensions : sa largeur, sa hauteur.
         Sur la feuille de papier, le bonhomme est donc une figure qui se développe dans un espace à deux dimensions.
         Si vous vous mettez face à la feuille, vous voyez bien ce qui est fait et vous admettez qu'il est en train de se réaliser une chose cohérente, régulière (puisque le dessin se fait toujours à la même vitesse), et sensée. Si l'on vous demande ce qui se fait, vous répondez qu'il se dessine un bonhomme.
 

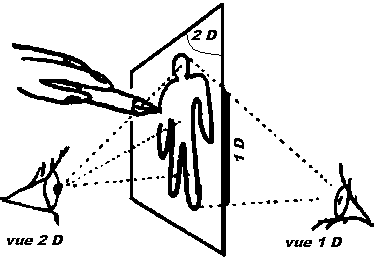
         Pour que les protéines du chromosome déroulé forment des figures continues alors que nous les voyons apparemment dispersées dans l'espace, comme dans ce petit exemple du bonhomme, il suffirait de penser qu'une dimension nous manque pour voir le phénomène réel tel qu'il se déroule.
         Pour cela, nous allons formuler l'hypothèse que la notion de dimension dans un phénomène ne se confond pas avec la notion des dimensions de l'espace où se déroule ce phénomène. Nous proposerons que le nombre des dimensions d'un phénomène soit le nombre des forces qui interviennent simultanément pour le produire.
         Nous montrerons par exemple comment l'univers peut développer des phénomènes à deux dimensions (c'est-à-dire produits par l'interférence de deux forces distinctes) aussi bien dans un fil qui n'a qu'une seule dimension d'espace, que sur une surface qui en a deux, ou que dans un volume qui en a trois.
         Nous suggèrerons que, pour penser les phénomènes de façon similaire à la façon dont l'univers les produit, il faut penser que les dimensions de l'espace ne sont que des cas très particuliers de ce que l'on doit entendre par dimension.
 
 

Dans le cas des chromosomes démêlés, nous montrerons qu'il s'agit d'un cas tout à fait banal d'interférence entre quatre phénomènes distincts se déroulant simultanément, donc un cas de phénomène à quatre dimensions.            Comme l'espace n'a que trois dimensions, en regardant ce qui se passe dans l'espace, on se retrouve avec une dimension de moins qu'il n'en faut pour voir ce que fait réellement l'ADN.               Cela ne dérange pas l'ADN ni les molécules qui continuent leur simple routine magnétique en quatre dimensions.            Comme cela n'empêchait pas de dessiner le bonhomme en deux dimensions, quand vous ne pouviez en voir qu'une seule.

         Parce que c'est une règle générale dans l'évolution de la pensée humaine : elle part toujours du concret, et met toujours très longtemps pour se débarrasser des entraves à la compréhension qu'implique cette origine concrète.
 
 
         C'est exactement ce qui est arrivé au chiffre 0 :
 
         Tout le monde sait compter 0, 1, 2, 3, etc. Les enfants apprennent cela très tôt à l'école.
         Pourtant, tous les grands penseurs mathématiciens de l'antiquité grecque (même Pythagore, même Euclide, même Thalès), ont pensé les nombres et calculé les nombres sans se servir du 0 qu'ils ne connaissaient pas. Qu'ils n'imaginaient pas. Ils avaient une notion encore trop concrète des nombres, trop rattachée à leur origine qui était de servir à dénombrer les choses : on a 1 chose, on a 2 choses, etc.
         Lorsque les anciens grecs croyaient réfléchir purement abstraitement sur les nombres, inconsciemment ils continuaient en fait à dénombrer quelque chose : une quantité ou une longueur. Lorsqu'il n'y avait pas de chose à dénombrer, il n'y avait pas besoin de chiffre pour dire combien on en avait. Avoir 0 quelque chose, n'avait donc pas de sens pour eux.
         En Occident, on n'a pas imaginé le zéro avant le IXe siècle environ, quand il nous a été apporté par les mathématiciens Indiens.
         Le zéro pourtant, ce n'est pas rien comme simplification. Il suffit d'essayer de faire des multiplications avec des chiffres romains, pour comprendre la difficulté qu'il y a de calculer sans zéro.
 

         Il n'y a pas que le zéro. Prenez par exemple les nombres négatifs :
 
         Il nous sont familiers, on les apprend aux enfants. Il nous manque 3 choses, on en a donc "-3".
         De Descartes, on connaît le philosophe, mais on oublie trop souvent qu'il fut un mathématicien hors paires. Il connaissait le zéro, et trouvait normal et évident que le zéro existe. Mais que pensait-il des nombres négatifs ? Pour lui, des nombres "moindres que rien" ne pouvaient qu'être insensés.
         N'est-ce-pas étonnant avec le recul, que les nombres négatifs n'aient été acceptés par les mathématiciens que depuis 2 siècles environ ?
         Toujours le même handicap : les nombres restaient encore trop attachés à des données concrètes. N'avoir aucune chose, pouvait maintenant se concevoir, c'était devenu une éventualité réelle que l'on pouvait représenter par le nombre zéro. Mais compter le nombre d'absences de quelque chose, cela n'avait pas de matérialité, c'était donc considéré comme irréalisable.
         Il a fallu que les humains pensent encore plus abstraitement la notion de nombre, pour admettre la possibilité de nombres négatifs. Il a fallu qu'ils détachent encore davantage le fonctionnement des nombres de toute donnée concrète tirée de leur expérience humaine.
         Il a fallu qu'ils apprennent à faire fonctionner toutes les propriétés abstraites que pouvaient porter les nombres, propriétés qu'ils portent précisément du fait de leur caractère abstrait. Il a fallu qu'ils ne se bornent pas aux fonctionnements des nombres qui ont un équivalent dans le fonctionnement simpliste des choses de tous les jours.
         Le fonctionnement de l'univers concret, se révèle finalement toujours plus abstrait que la pensée humaine.
 
 
 
         Ce qui est proposé c'est de faire pour les dimensions le même effort d'abstraction que celui fait par nos ancêtres pour penser les nombres indépendamment de toute donnée immédiate à mesurer, pour les penser et pour les faire fonctionner dans leur logique propre.
         Pour les dimensions, notre expérience quotidienne immédiate, c'est notre corps qui se déplace dans un espace à trois dimensions, avec une dimension de largeur, une de hauteur et une de profondeur du lointain.
         C'est de cette expérience-là dont nous devons nous abstraire.
         Des scientifiques ont supposé que l'univers puisse avoir jusqu'à dix ou seize dimensions. Même eux sont trop restés dans le concret, car ils ont imaginé les dimensions supplémentaires aux trois habituelles, comme étant seulement des dimensions d'espace en plus.
 
 
 
         Il faudra abandonner l'idée qu'une dimension est forcément une dimension d'espace, et qu'elle se mesure forcément par une longueur que l'on repère sur un axe gradué.
         Après cet effort d'abstraction, il sera possible de penser les figures des protéines de l'ADN en quatre dimensions, et même d'envisager un procédé pour voir ces figures dans leurs quatre dimensions.