 accueil
|
|
liste des effets propres à ce paradoxe 
|
tableau
|
9 - continu / coupé
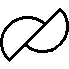
effet analytique
a8
   des
formes très autonomes les unes des autres subissent comme
miraculeusement les mêmes transformations lorsqu'elles sont
coupées par une même autre forme qui les traverse toutes
1 - cet effet s'appuie sur le paradoxe n° 8  synchronisé / incommensurable :
il n'y a pas de rapport de cause à effet que nous puissions
établir entre le fait que les formes sont traversées par
une autre forme continue et le fait qu'elles se transforment
brutalement à l'occasion de cette traversée
2 - l'appui fonctionne à l'aide du paradoxe 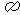 continu / coupé : il est lui-même en cause dans l'appui, ce qui implique que le continu et le coupé
correspondent à des formes différentes et que le continu n'est jamais lui-même coupé
3 - il s'organise au moyen du paradoxe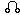 
lié / indépendant : les formes indépendantes sont
reliées par la forme unique qui les traverse en continu
4 - il est noué par le paradoxe clef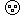 
même / différent : la traversée par une forme
continue est l'occasion d'établir une différence entre
les deux parties de chacunes des formes ainsi traversées
Justification du caractère analytique de type lecture :
il faut choisir de lire que les formes sont continues ou bien choisir
de lire qu'elles sont coupées par le fait de leur mutation
à l'endroit de leur traversée |
l'exemple de référence
Cas d'une mutation de couleur :
étape D0-31 - Juan Miro (1893-1983) : autour
des années 1940, Miro a beaucoup utilisé le principe
schématisé ci-dessous, au point d'en faire le
thème principal de certaines de ses toiles, telle "La
poétesse" de 1940. Ce principe consiste à dessiner une
ligne, et à peindre des formes, souvent
géométriques, à cheval sur cette ligne, en
changeant brutalement la couleur de cette forme au passage de la ligne.
La ligne qui traverse pourrait tout aussi bien laisser seulement son
tracé noir marqué sur les formes ainsi traversées,
et comme cette arbitraire mutation de couleur se répète
sur toutes les formes ainsi traversées, quelle que soit la
couleur de cette forme et quel que soit son dessin, la synchronisation
de la mutation avec le passage de la ligne nous apparaît
surprenante, comme si la ligne disposait d'une baguette magique pour
transformer la couleur d'une forme à l'endroit même de sa
traversée
Cas d'un éclatement d'une ligne en multiples brins :
étape D0-32 - Paolo Portoghesi (né en 1931) -
détail d'une des colonnes portant la coupole de la
mosquée du centre islamique de Rome (1976) : les
bandes qui montent du sol puis forment une tresse sous la coupole en se
rejoignant d'un pilier à l'autre, lorsqu'elles traversent un
anneau continu qui les coupe toutes, brusquement se divisent chacune en
plusieurs brins tout en changeant le sens de leur courbure, et tout
cela en parfaite synchronie. Cette synchronie nous surprend, car rien
dans la forme des rubans ne prépare à ce que leur coupure
par cet anneau continu soit l'occasion de leur éclatement en
multiples brins, ni à ce qu'elles changent brusquement de sens
de courbure exactement au même moment - source de l'image : Contemporary European Architects v.2, édité par Taschen (1994)
utilisation aux époques préhistoriques
utilisation aux époques anciennes
utilisation aux époques plus récentes
utilisation à l'époque contemporaine
dernière mise à jour de cette fiche : 7 novembre 2004
accueil
|
haut
|
liste des effets propres à ce paradoxe
|
|