 évolution
du mobile de A vers B
évolution
du mobile de A vers B
dans 4 dimensions simultanées
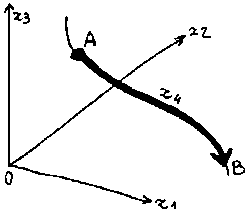
C'est le dessin de la portion de courbe continue AB qui représente la continuité de la 4ème dimension, souvent utilisée pour représenter la dimension du temps
| I
accueil |
E
sommaire Mathématique |
avant
: E
naissance d'une dimension |
suite
: F
dimensions en chaîne |
| accès direct à tous les autres textes de la section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
Pour voir ce qui se passe dans la 4ème dimension
Combien de dimensions peut-on représenter
et lire en continu ?
On a dit 3 pour l'espace, mais si
l'on ajoute la dimension du temps, cela fait 4.
Pour obtenir ces 4 dimensions on
construit un repère de 3 dimensions de coordonnées, et dans
ce repère on représente la position d'un mobile à
divers moments. C'est un repère 3 D + T classique, et le fait que
l'on y "retient" les unes à côté des autres les positions
successives prises par le mobile dans son déplacement permet d'y
figurer la 4ème dimension, celle du temps.
 évolution
du mobile de A vers B évolution
du mobile de A vers B
dans 4 dimensions simultanées C'est le dessin de la portion de courbe continue AB qui représente la continuité de la 4ème dimension, souvent utilisée pour représenter la dimension du temps |
On peut
donc envisager d'utiliser un tel graphique à 3 + 1 dimensions, pour
représenter les 4 dimensions d'une déformation 4 D + T, à
condition de renoncer à représenter en même temps leur
dimension de temps.
Dans le cas d'un phénomène
qui prend une 4ème dimension d'autosimilarité, c'est ce qui
se passe en continu dans cette dimension d'autosimilarité qui pourra
être représenté au détriment de ce qui se passe
en continu dans la dimension du temps.
Et l'on comprend maintenant que c'est
très exactement cela qu'a obtenu l'équipe de Robert Shaw
dans son graphique qui "truquait" la série 1 D des intervalles de
temps du robinet qui goutte chaotiquement [revoirE
ce graphique].
Chaque dimension du repère
3 D (abscisse, ordonnée et hauteur) porte la valeur de tous les
intervalles mesurés, mais comme ces valeurs sont décalées
"d'un cran" entre chaque dimension, la continuité qui se crée
sur la 4ème dimension du graphique correspond à ce qui est
"transverse" à tous les intervalles de durée mesurés.
Et ce qui est transverse à la dimension du temps où ils se
sont créés, et qui est transverse à chacune des déformations
qui les ont créés, c'est précisément l'interférence
de ces déformations qui, dans cette phase du phénomène,
se trouve être autosimilaire.
Ce qui apparaît sur le graphique,
c'est donc l'allure de la déformation continue d'autosimilarité
provoquée par l'interférence entre les 3 déformations
initiales du phénomène.
Comme il n'y a de place sur
ce graphique qu'à 4 dimensions continues, la dimension d'autosimilarité
a pris la place de la dimension du temps,
à laquelle on a explicitement renoncé en utilisant des coordonnées qui groupent des intervalles de temps différents. Dans ce type de coordonnées, chaque intervalle de temps est, en effet, confronté avec son suivant et avec celui qui suit son suivant, de telle sorte que l'on saute ainsi par-dessus la stricte continuité des évènements qui se succèdent, on brise la logique 1 D de l'écoulement du temps. Alors, nécessairement, sur ce graphique 4 D (4 déformations), un point et son suivant dans le temps n'ont plus aucune relation de continuité, et donc aucune relation de proximité.
On en vient maintenant à l'allure
elle-même d'un graphique qui représente une dimension d'autosimilarité.
Quand la 4ème dimension d'un
repère de coordonnées 3 D + 1 D correspond au temps, elle
est représentée par une courbe continue. Tous les points
successifs de cette courbe se touchent, comme tous les instants successifs
du déroulement du temps se touchent.
Quand
la 4ème dimension
correspond à la dimension d'autosimilarité, on doit s'attendre
à ce qu'elle soit cette fois représentée par une figure
autosimilaire, car de la même façon qu'un trajet continu a
comme "image" une courbe continue, une dimension d'autosimilarité
doit avoir comme "image" une figure autosimilaire.
C'est bien précisément
ce que l'on obtient.
On ne peut pas l'observer dans le
cas de l'attracteur dessiné par l'équipe Shaw, car l'image
est trop "floue". Mais on sait que la figure obtenue est en fait une coupe
transversale partielle d'un attracteur qu'on appelle l'attracteur de Rössler.
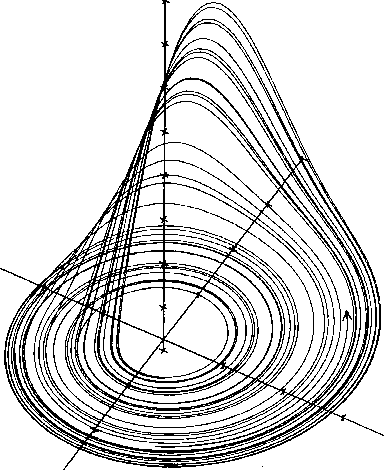 |
L'attracteur de Rössler le graphique
obtenu par l'équipe Shaw est en fait une coupe transversale partielle
de cet attracteur
[référence du dessin : James P. Crutchfield dans un article "le chaos" paru dans la revue Pour la Science"] |
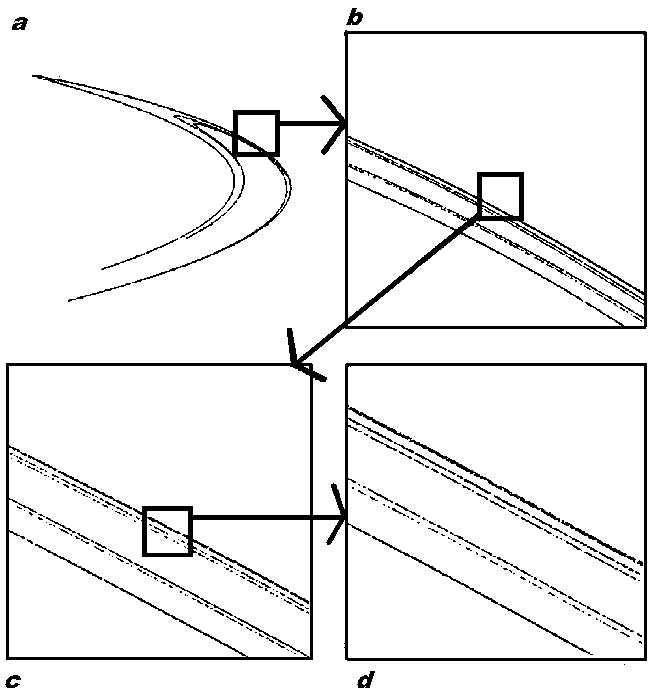
l'autosimilitude à toutes ses échelles de l'attracteur de Hénon [dessin de James P. Crutchfield] Cette courbe est calculée mathématiquement, et grâce à la simulation que permet le calcul, nous pouvons la regarder comme avec un microscope qui grossit jusqu'à 1000 fois. Ainsi, le dessin représente en a une vue d'ensemble de la courbe sur laquelle se situent les positions successives d'un même point de départ. En b, on a le petit carré de a grossi 10 fois. En c, on a le petit carré de b grossi 10 fois. Et en d on a cette fois le petit carré de c grossi 10 fois. En d, on a donc un détail de a agrandi 1000 fois, qui ressemble à la courbe d'ensemble a dans sa partie centrale. En même temps, d représente une partie des bandes de c, tellement similaire dans leur nombre et leur rythme d'alternance à la totalité des bandes de c ou des bandes de b (2 lignes très rapprochées sur le bord extérieur, 1 petit écart, 2 lignes assez rapprochées, 1 très grand écart, 2 lignes assez rapprochées, 1 moyen écart, 2 lignes extrêmement rapprochées formant le bord intérieur), qu'on ne peut pas faire la différence entre "une vue à une échelle" et "une vue à une échelle 10 fois plus petite" ou "100 fois plus petite", hormis pour ce qui concerne le rayon de courbure des figures. On a peine à réaliser que les 4 doubles lignes de la figure "d" ne sont que les grossissements des 2 doubles lignes les plus extérieures de la figure c. Et cela compris, on s'attend à ce que si la précision des arrondis de calculs permettait de grossir encore 10 fois le dessin, on trouverait dans l'agrandissement des 2 doubles lignes les plus extérieures de d, la même organisation en 4 doubles lignes. Quelle que soit l'échelle, le détail du détail est absolument identique au détail du détail du détail, etc. [nota : les simulations de l'attracteur de Hénon
montrent que la même allure autosimilaire se retrouve dans la partie
"en pointe" de la figure, avec d'ailleurs la même disposition des
bandes que dans la partie centrale. Ces deux parties ne se différencient
donc que par le rayon de courbure, qui est modéré dans la
partie centrale, et très brusque dans la pointe]
La forme est un aspect de cette figure.
On a expliqué plus haut à quoi ce déplacement chaotique du point est dû : la dimension de continuité dans le temps s'est effacée au profit de la dimension de continuité autosimilaire car le dessin ne possède pas assez de dimensions pour représenter en même temps ces deux continuités. |
| Maintenant tout semble
clair : on a dit qu'une
dimension d'autosimilarité avait dû naître brusquement
et chasser la dimension du temps, car il n'y a pas de place sur le graphique
pour les deux à la fois. On a bien trouvé sur le graphique
que la continuité du temps est brisée et qu'elle est remplacée
par une figure dotée d'un autre type de continuité, la continuité
de l'autosimilarité à toutes les échelles.
Pourtant, il reste encore un mystère. |
|
Il existe des attracteurs qui ne se présentent d'ailleurs pas du tout sous cette allure de bandes. Ainsi le graphique de "l'application logistique" dont nous donnons dans le dessin ci-contre plusieurs échelles d'agrandissement : les zones de points s'y regroupent seulement très vaguement, et l'on peut seulement appeler "ombrages" ces zones de plus forte densité qui n'ont aucunement l'allure de courbes. 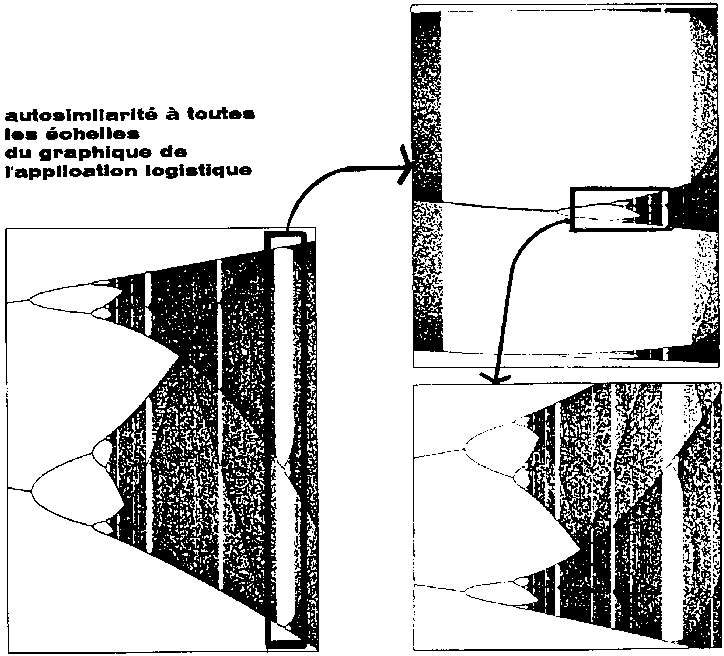 |
Les points des attracteurs étranges
se répartissent donc sur des surfaces de densités variées,
et non sur des courbes.
C'est le mystère qui reste
à éclaircir car cela ne va pas de soi.
On aurait
pu s'attendre à ce que la continuité dans la dimension d'autosimilarité
soit représentée par une courbe autosimilaire continue, de
la même façon que la continuité d'un trajet dans le
temps est représentée par une courbe continue.
Car des
courbes continues autosimilaires cela existe :
tous les trajets fractals que l'on a étudiés en sont des
exemples.
Un attracteur étrange pourrait
s'apparenter par exemple à la courbe que dessine un flocon de Von
Kock [revoir Ecette
courbe] plutôt
que de s'apparenter à la "courbe-surface" de Peano [revoirE
cette courbe-surface].
Qu'un point y fasse des
sauts discontinus dans le temps est une chose,
mais pourquoi saute-t-il
d'un point à l'autre d'une surface plutôt que d'un point à
l'autre d'une courbe ?
| I
accueil |
E
Math |
G
haut |
suite : F dimensions en chaîne |
|