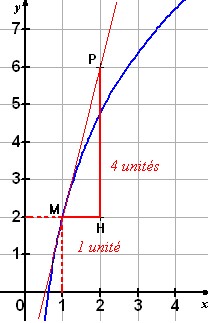
 La courbe en bleu est représentative
d'une fonction f. Elle admet une tangente en rouge au point M(1 ; 2)
La courbe en bleu est représentative
d'une fonction f. Elle admet une tangente en rouge au point M(1 ; 2)| f | fonction représentée par sa courbe (C) |
| f ' | fonction dérivée de f |
| f(x) | Image de la variable x. Sur le graphique c'est l'ordonnée d'un point de la courbe (C) |
| f '(x) | nombre dérivé. Sur le graphique c'est le coefficient directeur de la tangente à la courbe (C) au point d'abscisse x |
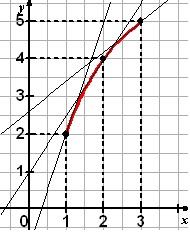 Voici par exemple une fonction f définie sur l'intervalle [1 ; 3] par sa courbe.
Voici par exemple une fonction f définie sur l'intervalle [1 ; 3] par sa courbe.