
ROBERT MARTY
Université de Perpignan

ROBERT MARTY Université de Perpignan |
||
Examinons maintenant le cas particulier de la diversité d'éléments.
La définition
4 se particularise facilement
puisque l'axiome
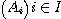 un élément D tel que: un élément D tel que:
Le diagramme correspondant est celui de la figure 11.
On remarquera que la diversité d'éléments sous-jacente à une unité d'éléments est susceptible d'une totalisation directe. Ceci explique comment les usages métaphoriques du terme "somme" peuvent conduire à voir le tout tantôt comme une entité dépassant l'ensemble des parties (cas de la définition 6) tantôt comme une entité restreinte par rapport à ce même ensemble (cas de la définition 4 dans laquelle l'axiome introduit une contrainte de "solidarité" entre les parties). On le conçoit bien en considérant nos exemples si l'on compare le groupe des personnes (totalité directe) avec la cellule familiale. Une famille peut être plus que le groupe sous-jacent si l'on évalue comme un enrichissement la prise en compte des relations familiales mais elle est d'une certaine manière moins que le groupe parce que ce dernier subit moins de contraintes institutionnelles par exemple. D'autres notions empruntées à la théorie des catégories peuvent se transposer sans difficulté. Citons par exemple les "totalités fibrées" qui permettent de formaliser des procédés de création d'entités nouvelles comme la formation des mots-valise dans la langue ou des créations graphiques comme certaines oeuvres de Escher ainsi que les "totalités inductives" qui permettent de formaliser des processus itérés à l'infini comme la semiosis peircienne. La notion de talité qui résulte de la dualisation de la totalisation présente un intérêt certain dans une perspective phénoménologique. |
| PRÉCÉDENTE | SOMMAIRE | SUIVANTE |