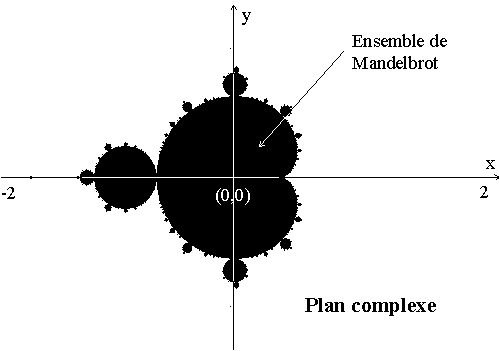
La Fractale de Mandelbrot

1. Introduction

Il s'agit sans doute de la plus connue des fractales dont la particularité est de présenter une variété infinie d'images pourvu qu'on se permette de l'agrandir autant que l'on veut. Je vais d'abord présenter l'objet mathématique pour ensuite expliquer la méthode de programmation et pour finir donner une idée de la façon d'explorer cet objet pour obtenir des images les plus variées possible.

2. De quoi s'agit-il ?

Pour définir mathématiquement la fractale de Mandelbrot on associe à chaque point du plan complexe, la suite z_n+1=z_n²+A avec z₀=0 et A=a+ib l'affixe du point. Tous les points pour lesquels la suite est bornée vont constituer l'ensemble de Mandelbrot.

Il est assez facile de démontrer mathématiquement que si le module de z_n est supérieur à 2 la suite va diverger. Ceci sera très utile dans la suite. On en déduit que l'ensemble de Mandelbrot est forcément inclus dans le cercle de rayon 2 et de centre (0,0).

Ceci permet de dire que l'aire de cet ensemble est finie (cf. Figure 1) alors que le périmètre lui est infini, ce qui est caractéristique d'un objet fractal. C'est donc à la frontière de cet ensemble que tout se passe et c'est là qu'il va falloir agrandir pour pouvoir calculer des images intéressantes.

Dans la pratique, ce qui nous permettra d'obtenir de belles images colorées, c'est d'associer une couleur aux points n'appartenant pas à l'ensemble de Mandelbrot selon leur rapidité à diverger. Cette couleur donnera une idée de la distance qui sépare le point de la frontière.

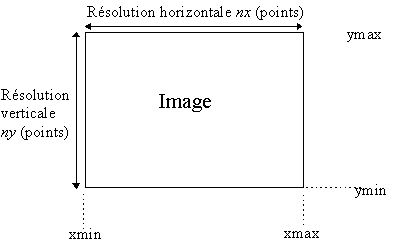
Figure 1 L'ensemble de Mandelbrot dans le plan complexe

3. Comment faire pour calculer une image ?

3.1. Calculs

3.1.1. Méthode

Il faut tout d'abord se donner les limites dans le plan complexe de l'image et choisir une résolution (nx ny) (Cf. Figure 2). Ceci fait, il faut boucler sur tous les points pour leurs appliquer l'algorithme de calcul qui déterminera oui ou non leurs appartenance à l'ensemble de Mandelbrot.

Figure 2 Définition du cadre et de la résolution de l'image

3.1.2. L'algorithme de calcul

Pour déterminer si un point fait partie ou non de l'ensemble de Mandelbrot on bouclera sur la suite complexe jusqu'à ce qu'elle diverge ce qui est acquis si |z_n|²= x_n²+y_n²>4 (Cf. Plus haut) ou que le nombre de boucles soit supérieur à une limite nmax fixée. Dans ce dernier cas, on supposera que la suite est convergente ce qui n'est pas forcément le cas. Il faudra choisir cette limite de façon réaliste pour que ça soit vrai à une fraction très faible près.

Les langages de programmation ne travaillent pas en général avec les nombres complexe. Avec z_n=x_n+iy_n on trouve la relation de récurrence sur les réels :
x_n+1=x_n²-y_n²+a
y_n+1=2 x_n y_n+b

3.2. Association des couleurs

On est maintenant en possession d'un résultat entier pour chaque point de notre image. Il s'agit maintenant d'y associer une couleur.

Si n=nmax+1 le point est convergent, on lui associe comme indice de couleur 0. Il faudra par la suite associer à cet indice une couleur qui se différentie bien du reste, on prend en général le noir.

Dans le cas n<= nmax il faut avoir une relation qui va faire correspondre un indice de couleur à chaque n. Si on dispose de NbC couleurs on peut par exemple prendre
Couleur=n modulo (NbC-1)+1 ou utiliser une fonction f qui fait correspondre l'intervalle [nmin,nmax] vers l'intervalle [1,NbC], on aura donc Couleur=f(n).

Dans les deux cas, on obtient un indice de couleur qu'il faut par la suite associer à une couleur réelle qui sera une composante tridimensionnelle de rouge, vert et bleu. Pour des raisons informatiques les indices de couleur sont pris en général entre 0 et 255 (8 bits) et de même pour le niveau de chaque composante de couleur primaire. Il faut donc créer un tableau de 3*256 octets qui vas composer notre palette de couleur.

3.3. Visualisation de l'image

Pour finir il faut maîtriser l'affichage des images (à partir des données et de la palette de couleurs) dans le système informatique dans lequel on se trouve ou maîtriser les formats d'image (GIF, JPG, BMP, etc. ...) pour pouvoir enregistrer les images calculées et les visualiser par la suite avec le logiciel adéquat.

4. L'exploration

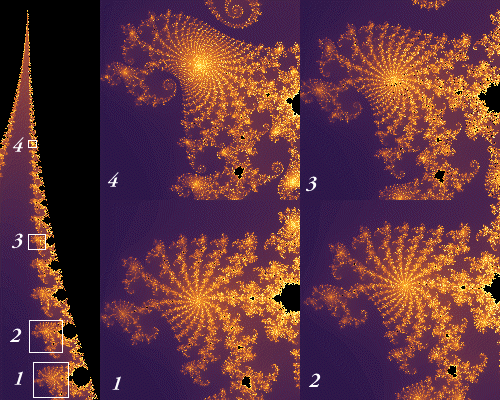
Figure 3 Progression d'une image le long d'un « bras »

Maintenant qu'on est outillé, il faut explorer l'espace complexe en commençant par calculer l'image de base (Cf. Figure 1) qui englobera tout l'ensemble de Mandelbrot. Tout ce qui est intéressant ce trouve dedans.

Ensuite, il s'agit de faire des zooms et d'explorer des zones de plus en plus petites pour voire apparaître de nouveaux objets. Pour cela, il faut sans cesse flirter avec la frontière et comprendre un peu la logique inhérente à l'objet mathématique qui va nous permettre en quelque sorte de nous guider.

Par exemple lorsqu'on progresse le long d'un « bras » de la fractale on voit progressivement la même image qui se répète mais avec chaque fois une petite modification (Cf. Exemple Figure 3). Cela peut être un bras de plus à chaque étape ou l'objet qui s'enroule autour de lui-même etc. De plus on voit régulièrement réapparaître l'image de base (Cf. Figure 4) qu'on peut aussi explorer pour découvrir les mêmes objets que dans l'original mais enrobés de ce qu'on pourrait qualifier d'une chevelure. Si vous n'avez pas saisi ce que je voulais dire rassurer vous c'est que mon vocabulaire est limité pour exprimer la diversité que peut engendrer la fractale de Mandelbrot. Le mieux c'est d'essayer pour comprendre.

Figure 4 Apparition de l'image de base après agrandissement

5. Conclusion

Je vous ai fait une présentation des plus classique. Il faut savoir qu'il existe de nombreuses méthodes de calcul s'appuyants sur différentes propriétés mathématique de la fractale. De même le choix des couleurs est infini, sachant qu'à cette étape c'est l'artiste qui intervient. Vous pourrez vous en faire une idée en explorant les nombreux sites sur le Web qui traitent du sujet.

Pour finir on peut se poser la question suivante : comment est-il possible d'engendrer des images aussi compliquées et variées avec une expression mathématique aussi simple ? Cela permet de faire le parallèle avec notre univers qui a atteint une complexité inouïe (l'homme) à partir des lois de la physique dont l'expression est très simple.