I-Trisection de l'angle
Ce problème remonte à l'antiquité. Malgré de nombreuses tentatives, ce problème resta longtemps irrésolu…
1)Quelques exemples
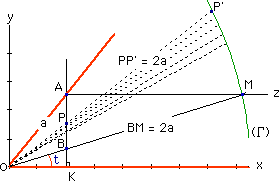
Nicomède proposa une solution approche de la trisection de l'angle par la construction d'une trisectrice : xA est l'angle que nous voudrions trisecter. Soit K le projet orthogonal de A sur [Ox) et [Az) la parallle [Ox) mene par A. Supposons plac sur [AK] le point B, tel que [OB) coupe [Az) en un point M pour lequel BM = 2OA.

En traitant la médiane issue de A dans le triangle BAM, on voit que ^AOB est le double de l'angle ^BOK. Ainsi l'angle ^xOM est le tiers de l'angle donne ^xOA : en effet, vu que BAM est rectangle en A, on a JA = JM = OA. Or ^BOK = ^JMA (alternes-internes). D'o , en notant t la mesure de ^BOK :
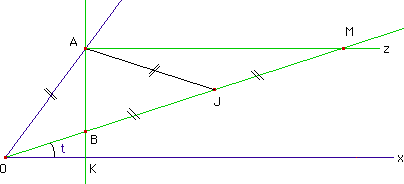
^AOB
= ^OJA = 2t, c'est dire que ^xOA = 3t.
Le problème est donc de déterminer M. Plaçons nous dans un repère orthonormé. Posons a = OA.
A tout point P situé sur [AK], on associe le point P' de [OP), tel que OP' = OP + 2a (donc PP' = 2a).
Tracez le plus grand nombre possible de demi-droites [OP) en reportant PP' = 2a.
Vous voyez se construire point par point la branche (ðG) de la trisectrice.
Cette construction étant achevée, la parallèle à (Ox) passant par A coupe (ðG) en le point M réalisant la trisection de l'angle ^xOA.
En notation moderne, l'équation polaire de la trisectrice ainsi obtenue est
r = OP + PP' = OK/cos t + 2a avec t compris entre 0 et pi/2
C'est une conchoïde (prononcer conkoïde ) de la droite (AK).
b)Ci-dessous, l'ordinateur a tracé la conchoïde (G) de la droite d'équation polaire r = 1/cos t (soit x = 1 en coordonnées cartésiennes) .
L'équation polaire de la courbe est :
r = 1/cos t + 2
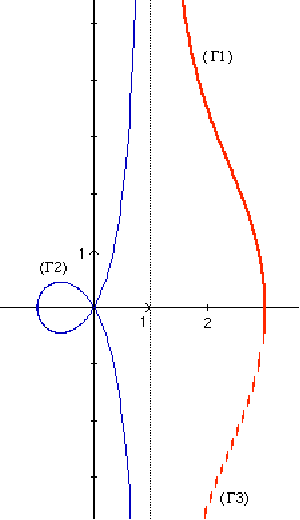
Le paramètre t varie de 0 à 2p. Les portions (G1), (G2) et (G3) correspondent respectivement aux intervalles [o,p/2] , [p/2,3p/2] et [3p/2, 2p].
2)Conclusion
Pour finir, c'est en 1837 que Wantzel conclut l'impossibilité de cette trisection. En effet, la trisection est impossible à la règle et au compas.
Par contre, le trisecteur permet de
partager un angle en 3 angles de même mesure.
Il se compose d'un triangle rectangle accolé à un demi-cercle,
dont le rayon a
même mesure que le petit côté de l'angle droit du triangle.
Quadrature
du cercle
Duplication
du cube