¿QUE ES UN ICONO-DIAGRAMA?

Un ícono-diagrama es un signo que representa a su objeto porque posee diádas de cualidades que ese objeto también posee.

Para saber más:

Peirce describe a los íconos-diagramas como "aquellos que representan las relaciones principalmente diádicas o consideradas como tales, de las partes de una cosa mediante relaciones análogas entre sus propias partes", lo que es rigurosamente equivalente a nuestra definición.
Ya hemos dado un ejemplo de íconos-diagramas: el del sistema nervioso de la rana que es un sinsigno icónico cuando un alumno lo produce, un legisigno icónico en su manual de biología. Las cualidades en cuestión son cualidades gráficas; el dibujo puede descomponerse en rasgos (curvas, segmentos, rectas) que uno trás otro de manera conveniente, constituyen el diagrama y poner dos rasgos uno tras otro es constituir una relación diádica entre las cualidades de cada uno de esos rasgos. Pueden citarse íconos-diagramas sonoros como todo lo que es música evoca cosas reales (por ejemplo "Pacific 231" de Arthur Honegger) y los niños los producen continuamente en sus juegos ( el revolver, y también la moto imaginaria que imitan produciendo simultáneamente íconos-diagramas sonoros y visuales). El ícono-diagrama gustativo queda ilustrado por la anécdota en la que un degustador profesional identificó una llave con su llavero de cuero caído en un tonel a partir de un sabor a hierro y a cuero.
Existe un género de ícono-diagrama que se llama ícono lógico que representa un papel fundamental en las ciencias formales y consecuentemente en las ciencias formalizadas. Toda fórmula de la física, toda fórmula de la química constituye un ejemplo de esto. 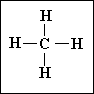Sea la fórmula que expresa la ley de Ohm U=RI; muestra que las medidas de tres magnitudes (representadas por símbolos remáticos U para la diferencia de potencial, R para la resistencia e I para la intensidad de la corriente) se vincula mediante dos relaciones diádicas _x_ (multiplicación) y _ = _(igualdad) de la siguiente manera _ = (_ x _)*. La fórmula desarrolladas del metano por ejemplo :

constituye un ejemplo aún más sorprendente.
Pero, quizás, es en álgebra en donde se encuentran las mejores ilustraciones en cuanto al interés de esta categoría de íconos para la comprensión de la actividad matemática. Sea el sistema clásico de dos ecuaciones con dos incógnitas
ax + by = c
a'y + b'y = c'
(con ab' - a'b diferentes de O)
muestra las magnitudes representadas por la letras x e y están en dos relaciones diádicas combinadas (suma e igualdad) (a_ + b_)= _ por una parte y (a'_ + b'_)= _- por otra. Resolver el sistema es mostrar que esas premisas son equivalentes a la conclusión según la cual esas mismas dimensiones están en las relaciones monádicas _= xo; _= yo mediante una serie de argumentos deductivos que aseguran la verdad de esta conclusión. Resolver ese sistema es operar sobre la configuración de las relaciones para destacar lo que está implícito en los datos, es decir mostrar que x=xo e y=yo.
Las figuras de geometría son, evidentemente, íconos-diagramas (legisignos) y buscar un problema de geometría es experimentar acerca de las réplicas de legisignos para deducir de una configuración inicial la verdad de la configuración pedida la que constituye la cuestión del problema.

(*)"_" representa un indicador de lugar.

Indice de la zona roja. Recorrido aconsejado.