Qu'est-ce que l'énergie ?

D'après notre hypothèse [voir E cette explication], l'énergie est ce qui oblige les ondes d'espace à se déformer, et qui rend permanente cette déformation locale en la faisant circuler sous forme d'une vibration qui se propage sans arrêt d'une onde à l'autre. Cette déformation locale qui court sans arrêt d'une onde d'espace à l'autre, on l'appelle photon.
Un photon est donc de l'énergie emmagasinée. Et l'on sait qu'un photon voyage à la vitesse de la lumière, que l'on appelle "c".
Pour avoir de l'énergie, il faut donc que les ondes stationnaires de l'espace se déforment, et que cette déformation circule de l'une à l'autre à la vitesse c.
Comme un photon voyage grâce à une vibration des ondes d'espace qui se déplace à la vitesse de la lumière, on peut en déduire que la vibration aller et retour des ondes d'espace va aussi à la vitesse de la lumière.
Bien qu'elles vibrent à la vitesse de la lumière, les ondes d'espace reviennent toujours au même endroit puisqu'elles font des allers et retours : leur vitesse globale est donc nulle.
En résumé, par rapport à cette vibration à vitesse globale nulle mais effectuée à la vitesse de la lumière, le photon s'éloigne sans cesse à la vitesse de la lumière des ondes sur lesquelles il passe.
 
  

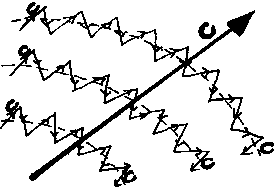Déplacement d'un photon à vitesse c par rapport à la vibration à vitesse c des ondes d'espace : un photon est donc quelque chose qui va c fois plus vite que quelque chose qui va à vitesse c, il va donc à la vitesse c² par rapport "à l'espace non vibrant".  Avoir un photon, c'est donc avoir du c² organisé, et parler d'énergie ou parler de c² revient donc strictement à la même chose.

On sait qu'un photon possède une énergie h, qui est la constante de Plank.
Si on appelle v la fréquence à laquelle nous arrive des photons, pour quantifier l'énergie qui nous arrive, il suffit d'écrire
    E = h x v , ce qui est la formule de Plank et Einstein qui sert à exprimer l'énergie d'un rayonnement.

Pour quantifier cette fois l'énergie que l'on a dans une particule de matière[voir E l'explication selon laquelle une particule de matière est une circulation en boucle fermée de neutrinos, qui eux-même sont des photons organisés en spirale], on ne peut pas utiliser la notion de fréquence d'arrivée de la matière, puisqu'elle peut être aussi bien fixe qu'en déplacement. Puisque l'énergie c'est du c², on peut dire simplement que l'on a dans toute matière une certaine quantité de c², et que cette quantité reste constante dans le temps. Si l'on appelle m, la masse, cette quantité de c² que l'on a dans une matière, on obtient la formule suivante :
        E = m x c²

Bien entendu tout le monde connaît la célèbre formule d'Einstein E = m.c², mais cette formule que nous retrouvons ici, nous devons en proposer un contenu tout autre que celui habituellement admis.
D'habitude en effet, on dit que cette formule signifie que l'on peut transformer de la masse en énergie, et inversement. C² joue dans cette interprétation seulement le rôle de constante, qui indique quelle quantité d'énergie on peut obtenir en transformant une masse m en énergie. On interprète donc habituellement cette formule comme :
        E = m en quantité c²
Notre interprétation nous a fait considérer au contraire que l'énergie était strictement la même chose que du c². Notre interprétation de cette formule est donc :
        E = c² en quantité m

Le résultat numérique de l'opération est bien entendu le même, mais sa signification profonde est changée. Ce que notre hypothèse montre, c'est que la masse n'est pas une réalité qui peut se transformer en une autre réalité : la masse n'est qu'un nombre, une grandeur. Inutile donc de chercher où se trouve la masse d'une particule, puisque la particule n'a pas réellement de masse : elle regroupe seulement une certaine quantité d'énergie que l'on peut mesurer avec le nombre que l'on appelle "masse". Pour ne pas créer d'ambiguïté, on ne devrait donc pas dire qu'une particule a une certaine masse, mais qu'elle mesure une certaine masse. De la même façon qu'on dit par exemple, qu'elle mesure une certaine longueur.

 
On peut s'interroger sur l'emploi du même nombre "m" que celui employé pour mesurer l'effet de gravité d'un corps.
On a expliqué [voir E cette explication] que l'effet de gravité est proportionnel à l'énergie des tourbillons que provoque une matière dans le vide autour d'elle. Que la quantité de ces tourbillons soit en rapport avec la quantité de neutrinos que la matière emmagasine, cela semble normal. Comme les neutrinos sont eux-mêmes fabriqués avec des photons [voir E cette explication], et que des photons sont du c², il est donc normal que l'effet de gravité soit proportionnel à la quantité de c² incluse dans la matière, donc à m.