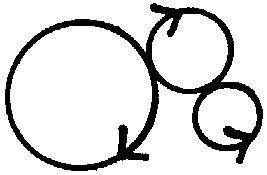I
accueil |
E
sommaire
Science |
|
|
|
avant
: E
une particule est à
l'espace ce qu'une vague est à la mer |
Mais où
est donc passée la gravité ?
À l'intérieur du domaine
de validité de chacune des forces, une équation, ou une série
d'équations, peut certainement décrire la régularité
du mouvement qui en résulte, et ce sont ces équations que
la science a progressivement mises à jour depuis Kepler et Galilée.
Chaque force naissant de la précédente
à l'occasion d'une coupure paradoxale[en
voir E
l'explication],
on peut cependant douter de la possibilité de décrire toutes
les forces par un même système d'équations, et si jamais
l'on y parvient, on peut douter de l'intérêt de cette trouvaille
purement anecdotique qui n'expliquerait ni la cause ni le mécanisme
de génération successive des forces l'une par l'autre.
Quant à décrire la
gravité par une même équation que les quatre forces
dont on a décrit [voir
E cette
description] la génèse
les unes par les autres, cela paraît d'autant plus improbable et
infécond que . . . l'on a même pas eu besoin de la gravité
pour décrire l'évolution globale de l'univers.
Selon
notre hypothèse la gravité ne serait pas une force fondamentale
: elle ne serait qu'un effet second, causé par l'existence même
de la matière et par sa façon d'exister.
La matière
crée des tourbillons dans les ondes d'espace qui l'entourent
On a supposé dans un texte précédent
que les particules de matière sont formées de neutrinos qui
tournent les uns derrière les autres. [voir
E cette
explication]
|
|
 selon
notre hypothèse, 3 neutrinos en boucle fermée triangulaire
= 1 quark up (l'une des "briques" du noyau des atomes) selon
notre hypothèse, 3 neutrinos en boucle fermée triangulaire
= 1 quark up (l'une des "briques" du noyau des atomes) |
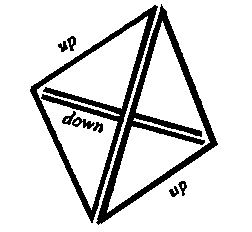 2
quarks up triangulaires et 1 quark down en va-et-vient forment ensemble
une structure tridimensionnelle : le proton d'un atome de matière 2
quarks up triangulaires et 1 quark down en va-et-vient forment ensemble
une structure tridimensionnelle : le proton d'un atome de matière |
|
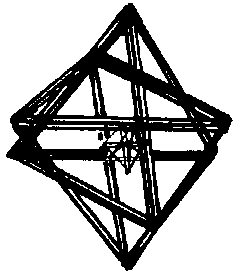 un
atome d'hélium 4, formé de 2 protons et de 2 neutrons tête-bêches, un
atome d'hélium 4, formé de 2 protons et de 2 neutrons tête-bêches,
avec
au centre 2 électrons tête-bêche.
Chaque
neutron est encastré dans un proton qui l'aide à tenir (il
manque une branche au neutron pour pourvoir tenir tout seul) |
En réalité, comme les neutrinos ne sont que des torsions
des ondes d'espace [en voir E
l'explication], la notion de leur déplacement
est toute relative. On n'a pas besoin de supposer que les neutrinos courent
réellement les uns derrière les autres. Ce qu'il faut entendre
par mouvement bouclé, c'est que les torsions des ondes d'espace
passent sans se défaire d'un neutrino à l'autre.
Ce qu'il importe maintenant de remarquer, c'est que tous ces mouvements
en boucles serrées, combinées et encastrées l'une
dans l'autre, forment finalement ce que l'on peut bien appeler "un tourbillon"
: un tourbillon de photons prisonniers d'un parcours en boucle qu'ils parcourent
en groupe à la vitesse de la lumière.
On avait donc décrit [voir
E cette
description] un photon comme une torsion des ondes d'espace
qui file en ligne droite à vitesse c sur ces ondes d'espace, et
l'on décrit maintenant une particule de matière comme un
tourbillon qui tourne sur place à la même vitesse c. Mais
une particule de matière n'est pas qu'un énorme paquet de
photons fixe, car la fixité change tout : un photon qui passe est
comme une vague qui passe sans rien laisser derrière elle, mais
une particule de matière qui bouillonne en permanence au même
endroit va forcément influencer durablement son environnement.
Que se passe-t'il en effet quand on forme un tourbillon permanent,
par exemple en mettant en marche une hélice de bateau dans une eau
calme ? : le tourbillon entraîne l'eau alentour, et la zone tourbillonnaire
s'enfle, s'agrandit jusque très loin du bateau. Car il y a une différence
de vitesse entre la vitesse du tourbillon et la vitesse nulle de l'eau
alentour, et une différence de vitesse engendre toujours un tourbillon
à la limite entre les deux zones. Ainsi, un tourbillon engendre
nécessairement d'autres tourbillons alentour de lui.
| De la même façon,
on doit penser qu'un tourbillon de matière crée autour de
lui des tourbillons plus petits, qui eux-mêmes créent des
tourbillons plus petits, et ainsi de suite. Jusqu'à ce que soit
complètement résorbée la différence de vitesse,
entre l'énorme vitesse c du tourbillon, et la vitesse globale dérisoire
de son environnement. |
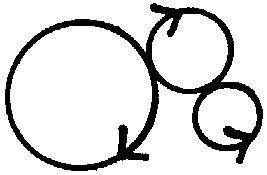 |
Où
l'on retrouve la gravité selon Newton
Quand la matière se forme dans la galaxie, la galaxie tourne
déjà [en voir E
l'explication]. Elle tourne parce qu'une
force y organise le mouvement systématiquement et à toutes
les échelles en spirale, depuis la plus petite échelle de
spirale que forme chaque neutrino jusqu'à la spirale générale
de la galaxie elle-même. Bref, quand la matière se forme pour
boucler en rond ce qui tourne déjà en spirale, cela tourbillonne
déjà et partout et sur toutes les échelles.
Pas plus que la matière n'est à l'origine du mouvement
tournant de la galaxie, la matière n'est donc à l'origine
de l'existence de tourbillons de déformation des ondes d'espace.
Comment les tourbillons engendrés autour d'elle par le mouvement
interne à la matière vont-ils influer sur le mouvement des
tourbillons spiralants déjà existants dans la galaxie ?
Venant "après", ils ne peuvent pas les contredire, car ceux
d'avant ont déjà la solidité indestructible que donne
l'autosimilarité à toutes les échelles. En outre,
leur source est bien faible et bien morcelée pour organiser un réseau
de tourbillons plus amples que ceux créés par le détournement
des jets énormes et compacts du quasar.
La matière ne crée donc pas son propre réseau
de tourbillons, elle s'appuie sur ceux déjà existants, et
les déforme autant qu'il le faut pour les assujettir à ses
besoins.
Dans ce but, la matière modifie leur vitesse et déplace
leurs sommets.
Commençons d'abord par la question de la vitesse
:
Les tourbillons spiralant qui font tourner la galaxie ont pour fonction
de réguler un différentiel de vitesse entre quelque chose
qui file à vitesse c (les jets de quasar) et quelque chose (les
ondes stationnaires) qui freine ce qui file parce que cela file trop vite.
Les jets du quasar se sont alors transformés en bras spiralant
de galaxie et tournent sous l'effet d'une composante qui les fait tourner
en rond. Comme les jets vont partout à la vitesse constante de la
lumière, la composante "qui tourne en rond" finit par s'égaliser
elle aussi et partout à une vitesse uniforme.
|
note : on rappelle que c'est cette vitesse
de rotation uniforme en tous points de la galaxie que l'on observe effectivement
dans la réalité, alors qu'elle est contraire à la
simple géométrie de la forme (pour que la spirale tourne
sans se déformer il faudrait que ses parties externes tournent beaucoup
plus vite que ses parties internes car elles ont beaucoup plus de trajet
à parcourir pour chaque rotation) et qu'elle est aussi contraire
à un fonctionnement selon les lois de la gravité (à
l'inverse la gravité voudrait elle que ce soient les parties internes
qui tournent plus vite que les parties externes, ce qui est nécessaire
pour qu'elles puissent échapper à l'attraction du centre
de la galaxie qui est plus forte près du centre qu'à la périphérie) |
Dans la matière cela circule à la vitesse c. Comme on l'a
vu plus haut cette circulation interne génère des tourbillons
autour de la matière, et très normalement ont peut deviner
que la matière les fait tourbillonner aussi à la vitesse
c.
C'est tout du moins ce qui se passe tout près de la matière,
car loin d'elle, les tourbillons sont seulement entraînés
par la force qui fait tourner la galaxie et vont naturellement à
la vitesse constante de rotation de la galaxie.
La présence de matière génère donc le besoin
d'amortir un différentiel de vitesse, et quelque soit la quantité
de matière en cause et la position de cette matière dans
la galaxie ce différentiel est le même : il s'agit toujours
d'accélérer la vitesse pour passer de la vitesse constante
de rotation de la galaxie jusqu'à la vitesse constante de la lumière.
Au fur et à mesure que la matière s'installe dans la
galaxie elle réorganise les vitesses pour que ce mouvement d'accélération
depuis une vitesse constante vers une autre vitesse constante s'uniformise
à toutes les échelles, ce qui ne peut se faire que si cette
accélération elle-même est régulière.
La présence de matière produit donc une déformation
élastique des tourbillons spiralant qui lui préexistaient
dans la galaxie, de telle sorte qu'ils impulsent maintenant une accélération
uniforme et constante vers la matière. On
retrouve donc là et de façon toute naturelle, l'un des paramètres
de la loi de gravité universelle de Newton : la présence
de matière provoque vers elle une accélération uniformément
accélérée.
Examinons maintenant la question de l'intensité
:
Si un temps suffisant lui est donné, l'effet de gravité impulsé par une matière s'uniformise dans tout
le volume qui entoure cette matière, mais cela doit être considéré sur une échelle globale, de telle sorte que l'intensité de l'effet des tourbillons se répartit sur la
surface d'une sphère qui est de plus en plus grande au fur et à mesure que l'on s'éloigne du centre de la matière.
Comme la surface d'une sphère varie comme le carré de
son rayon, l'intensité de l'accélération
de la gravité varie donc en fonction inverse du carré de
la distance à la matière. Et l'on retrouve là, un
deuxième paramètre de la loi de Newton.
Examinons ensuite la question de l'ampleur de la force
:
On peut se douter que plus il y aura de neutrinos rassemblés
en circuit fermé, donc plus de matière au même endroit,
plus les tourbillons qu'ils entraînent seront forts.
Si l'on appelle "masse" cette quantité de neutrinos, on
retrouve la proportion directe entre la masse d'un corps et l'intensité
de l'attraction gravitaire qu'il exerce sur les autres, ce qui est un troisième
paramètre de la loi de Newton.
Revenons pour finir sur la question de l'accélération
:
Comme le différentiel de vitesse à encaisser se fait
toujours entre la vitesse constante de la galaxie et la vitesse constante
c de la lumière, l'accélération imprimée est
toujours la même, quelle que soit la quantité de matière
en cause. On retrouve ici le dernier
paramètre de la loi de Newton, selon lequel l'accélération
d'une masse est indépendante de sa taille : dans le vide, une petite
bille tombe aussi vite qu'un gros boulet.
Où
l'on retrouve la gravité selon Einstein
Examinons maintenant comment la matière déplace les sommets
des tourbillons spiralants qui font tourner la galaxie pour les faire coïncider
avec ses propres besoins.
Quand la terre par exemple tourne autour du soleil, on sait qu'elle
décrit une ellipse dont le soleil occupe l'un des foyers.
On sait démontrer en géométrie, que l'ensemble
des cônes qui passent par une ellipse ont tous leurs sommets rassemblés
sur une hyperbole située dans un plan perpendiculaire à l'ellipse
et passant par l'un de ses foyers.
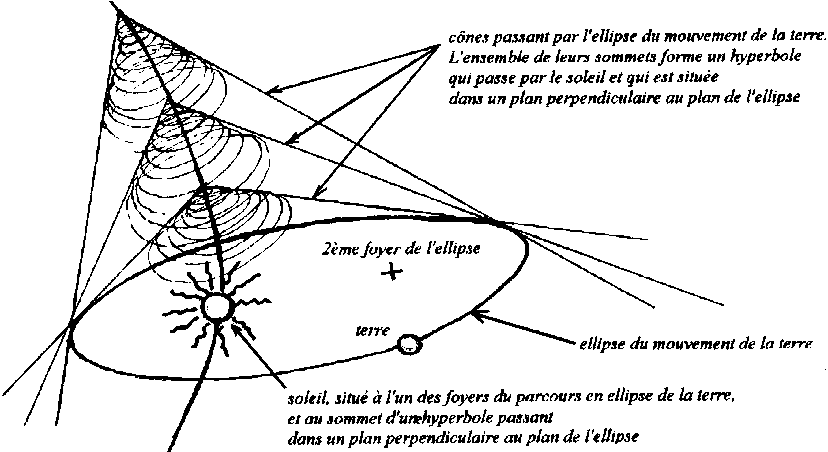
On peut donc supposer que pour entraîner la terre dans une ellipse,
le soleil mobilise des tourbillons spiralants à toutes les échelles,
et que ces tourbillons forment des cônes dont les sommets sont situés
sur une hyperbole passant par le soleil.
De façon symétrique, on doit penser que la terre mobilise
des tourbillons spiralants qui forment des cônes qui s'appuient tous
sur une même hyperbole, et dont tous les sommets occupent l'ellipse
de son parcours.
Ainsi, autant que la terre tourne
en ellipse autour du soleil, le soleil parcourt donc une hyperbole "au-loin"
de la terre.
Constater cela, c'est constater
que la terre fait lentement sortir le soleil du plan de son ellipse pour
lui faire suivre cette hyperbole. Cela explique pourquoi
la loi de Newton qui décrit le mouvement de la terre dans un plan
d'ellipse fixe, n'est pas absolument exacte. Comme l'a montré Einstein,
pour calculer exactement la trajectoire de la terre, il faut faire intervenir
des calculs dans ce que les mathématiciens appellent le "plan complexe".
Or ce plan complexe a précisément des propriétés
hyperboliques.
Une masse
courbe-t'elle vraiment l'espace-temps ?
Pour Einstein la gravité n'était pas une force comme
les autres. Pour lui ce n'était même pas une force du tout,
mais seulement un effet dû à une particularité géométrique
de l'espace-temps : la présence de masse déformerait l'espace-temps
de telle sorte que le trajet d'une matière où d'un rayon
lumineux passant à proximité se trouverait détourné,
dévié par cette présence.
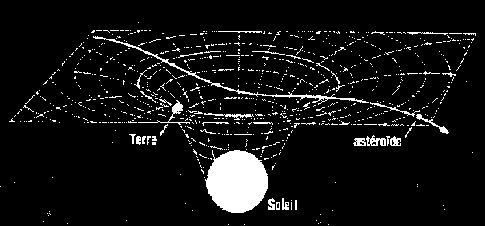 |
Un
exemple de représentation conventionnelle de la courbure de l'espace-temps
par une masse qui s'y trouve, en l'occurence on voit ici la déformation
de la trajectoire d'un astéroïde par la présence du
soleil.
On
remarque que l'espace-temps qui possède 4 dimensions est réduit
à la représentation de seulement 3 dimensions.
[Document
revue Sciences et Avenir] |
Le fait physique en lui-même n'a jamais été éclairci
: comment donc la masse d'un corps s'y prend-t'elle pour courber l'espace
? On n'a jamais vu la masse d'un corps, on n'a aucune hypothèse
sur l'endroit où elle peut se loger dans une particule, et on n'a
aucune idée du processus physique qui permettrait à une masse
de courber l'espace.
La seule chose qu'Einstein a montré, c'est que pour calculer
avec précision l'effet de la gravité il ne faut pas le calculer
selon les règles de Newton mais calculer la déformation de
son trajet par un calcul de courbure de l'espace-temps.
On se trouve donc en présence de deux réalités
certaines :
1- la présence
d'une masse fait se rapprocher d'elle les autres masses et les rayonnements
2- pour calculer cet
effet il faut calculer une déformation géométrique
de l'espace-temps
De ces deux réalités que nous ne remettons en cause ni
l'une ni l'autre, les scientifiques tirent habituellement la conclusion
: donc une masse déforme géométriquement
l'espace-temps.
Autrement dit : "puisque cela se calcule comme
cela, cela se passe comme cela".
Ce raisonnement n'est d'ailleurs jamais réellement fait, il est
seulement implicite car il ne semble même pas utile de discuter son
bien fondé : cela va de soi.
Et bien non ! cela ne va pas de soi.
S'il faut calculer une déformation géométrique
de l'espace-temps pour calculer l'effet de la gravité, c'est que
l'on est en présence de l'un ou l'autre des deux cas de figure suivants
:
1- soit les masses
déforment réellement l'espace-temps et le calcul rend bien
compte de cet effet
2- soit nous n'avons
pas d'autre solution pour calculer que de tordre les axes de coordonnée
utilisés, ce qui revient à faire "comme si" l'espace-temps
était tordu
Notre hypothèse est que nous sommes dans le cas 2-, ce que nous
allons tenter de justifier maintenant.
Chose caractéristique, quand on veut illustrer comment une masse
courbe l'espace, on ne représente pas l'espace 3 D dans toutes ses
3 dimensions comme il est dans la réalité, mais seulement
un plan 2 D dont on voit le grillage régulier se déformer
par l'effet de la gravité et se transformer en panier de basket-ball
[voir le dessin reproduit un peu plus haut].
Et l'on nous dit que la particule qui passe dans ce genre d'espace
suit nécessairement le chemin courbe sur la surface déformée
qu'elle doit traverser.
On n'oublie pas de nous rappeler que bien sûr on a représenté
l'espace 3 D par un plan 2 D, mais que cela se passerait de la même
façon s'il y avait 3 dimensions de représentées, mais
qu'on ne peut vraiment pas dessiner sur un dessin 3 D la courbure d'un
espace 3 D.
|
note : encore ne s'agit-il dans ce cas
que d'enlever une seule dimension à l'espace, mais souvent les physiciens
sont plus radicaux et partent dans des considérations fondamentales
sur la nature et le sort de l'univers en commençant comme ceci :
soit en horizontal la dimension du temps, et en vertical les dimensions
de l'espace. On appelle cela un diagramme d'espace-temps, et pourtant il
n'a que 2 coordonnées pour mesurer ses 4 dimensions.
C'est ce type de réduction de l'espace réel 3 D à
un plan fictif 2 D qui est utilisé pour démontrer que la
supposée expansion symétrique de l'univers de tous les côtés
autour de nous n'implique pas nécessairement que nous soyons au
centre même de l'univers : depuis tous les points de l'univers on
pourrait faire la même observation car l'expansion devrait se comprendre
comme celle d'un ballon qui augmente de volume et dont tous les points
de la surface s'écartent de la même façon l'un de l'autre
et voient tous de la même façon les autres s'éloigner.
Oui certes, mais à condition de réduire l'univers à
une surface et d'oublier le vide au centre du ballon et le vide tout autour
de lui.
Jusqu'à preuve du contraire l'univers occupe un espace en
trois dimensions, et tant que l'on a pas démontré que l'une
de ces dimensions peut être négligée, on doit s'abtenir
de ce type de raisonnement qui nie dès la départ l'une des
propriétés fondamentales de l'univers. |
Or, tout le problème vient précisément de cette question
de "ce qu'est une dimension", et de "comment une dimension peut se représenter
en mathématique".
On nous apprend très tôt à ne pas faire d'additions
mélangeant les choux et les carottes, mais on nous apprend à
additionner ou à multiplier les nombres de la même façon
selon qu'ils représentent des longueurs, des surface ou des volumes.
Cela marche souvent, précisément parce qu'on fait toujours
ces calculs dans les cas "où cela marche", mais fondamentalement
cette façon de procéder dénature les nombres et leurs
propriétés qualitatives différentes selon qu'ils représentent
des grandeurs à 1, 2, 3 ou 4 dimensions.
On sait depuis la 2ème
loi de Kepler, que le mouvement de la terre autour du soleil se caractérise
par le fait que lors de son mouvement en ellipse la terre découpe
des secteurs de surfaces égales pendant des durées de temps
égales. La gravité a donc à voir avec la
conservation d'une grandeur de surface (2 D) au cours du temps, alors
qu'on cherche à la calculer à l'aide de coordonnées
qui ne sont que des longueurs (1D) sur des axes.
Si multiplier des m² se fait comme multiplier les m, cela est
sans importance. Mais si les valeurs de surface se mulitplient d'une façon
plus complexe que les valeurs de longueur, alors le résultat sera
faussé. Notre hypothèse est que la valeur de "la masse" que
l'on utilise pour faire les calculs de gravité est une grandeur
qui porte en elle deux dimensions simultanées et inséparables,
cela parce que la masse est elle-même une valeur de produit (voir
à la page E = c², en quantité
m où l'on montre pourquoi la masse m serait la mesure d'une
certaine quantité de c², donc le produit de la vitesse de la
lumière par la vitesse de la lumière).
La courbure de l'espace euclidien conventionnel du calcul d'Einstein,
proviendrait alors simplement du fait que l'on veut mesurer un phénomène
de dimension 2 par des axes qui ne peuvent mesurer qu'une seule coordonnée,
donc une seule dimension à la fois. Le calcul selon Einstein se
fait à l'aide de nombres dit "complexes" parce que chacun possède
deux coordonnées, et dans cet espace là du calcul des nombres
complexes, qui est un espace conventionnel de calcul, le calcul fait s'accorde
avec ce que l'on suppose de la masse : c'est une grandeur à deux
dimensions qui a besoin de deux dimensions simultanées pour être
mesurée. Dans cet espace conventionnel des nombres complexes, la
masse se comporte effectivement comme une grandeur qui déforme l'espace-temps.
Le problème est lorque l'on "ramène" cela à l'espace
normal en faisant comme si l'espace conventionnel des nombres complexes
inventé par les mathématiciens était analogue à
l'espace-temps réel. C'est possible.
Mais il existe une autre possibilité que nous soutenons : les
coordonnées que nous utilisons pour mesurer le temps et l'espace
dans notre univers sont des grandeurs 1 D qui "applatissent" la valeur
que porte la masse d'un corps, parce que la masse d'un corps est un nombre
qui porte la dimension 2, et qu'on ne peut pas la mesurer par un axe sans
lui faire perdre une partie de ses propriétés. Pour
compenser l'applatissement de la valeur de la masse, il conviendrait donc
de creuser l'axe d'espace conventionnel utilisé dans le calcul :
on déforme en prenant un repère d'axes qui ne sont pas appropriés
à la mesure, et l'on compense notre déformation en imprimant
conventionnellement au repère une déformation inverse.
La courbure de l'espace par les masses ne serait
donc pas dans la réalité de l'univers, elle serait une simple
nécessité de calcul. Nous nous sommes utilement fabriqué
des lunettes déformantes pour calculer les mouvements de la matière
dans l'espace mais nous devons enlever ces lunettes dès lors qu'il
ne s'agit plus de calculer mais seulement d'observer.
Einstein nous a aidé à voir clair sur le calcul permettant
de mesurer la réalité. Il nous a probablement aveuglés
en supposant que ce calcul procédait de façon similaire au
fonctionnement même de l'univers.
|
Pour plus de développements sur cette question
centrale, on renvoit à :
F
la question des dimensions (la façon dont nous posons
le problème en introduction au livre "l'adieu au Big-Bang")
F
la section mathématique de ce site (cette section
est tout entière consacrée à montrer comment les nombres
ont par eux-mêmes des dimensions, et comment le reconnaître
modifie notre interprétation des phénomènes physiques) |
Feu la
gravité universelle, y compris à l'intérieur du système
solaire
Pas plus que nous n'avons donné
d'importance à la gravité pour générer les
galaxies, nous ne lui donnons d'importance pour initier une étoile
et son cortège planétaire : ce ne serait
pas sous l'effet de la condensation par gravité d'un nuage moléculaire
que naîtrait une étoile, mais sous l'effet du démarrage
d'un micro-quasar au sein d'un tel nuage.
Ce qu'a observé
le téléscope spatial Hubble, c'est qu'effectivement la naissance
d'une étoile donne lieu à l'émission de deux violents
jets symétriques analogues à ceux d'un quasar.
Ce serait donc le même processus
que celui qui fait tourner la galaxie qui mettrait en branle la ronde des
planètes autour de l'étoile, mais la force des tourbillons
spiralant qui font tourner cherche cette fois à croitre dans un
contexte où règne déjà la matière et
la gravité. Cela expliquerait pourquoi la gravité prend rapidement
le dessus à cette échelle, et pourquoi c'est la gravité
qui continue à sa façon ce mouvement tournant qu'elle n'a
pas généré.
Les anneaux qui entourent certaines
planètes comme Saturne, constituent un moment intermédiaire
dans cette évolution entre le règne du mouvement en spirale
généralisé et le mouvement en rond généralisé.
On y trouve en effet des "arcs de matière" qui sont tout à
fait contraires à la loi de la gravité car ils devraient
être rapidement étalés et laminés s'ils tenaient
et tournaient selon cette loi.
Pour notre explication ces arcs
rebelles à la gravité ne sont pas un mystère : ils
sont les vestiges du mouvement qui préexistait à la matière,
des morceaux de spirale que la matière n'est pas assez forte pour
assujettir à son propre mouvement.
image
: vue d'artiste des arcs de matière qui ont été repérés
dans le plan d'un anneau de la planète Saturne. La "loi" de la gravité
voudrait que ces arcs soient rapidement étalés et disloqués
au cours de leur rotation autour de la planète. La "loi" de la gravité
est donc prise en défaut à l'intérieur même
du système solaire.
[d'après
un document de la revue Ciel et Espace de mai 1993]
|

Même
à l'intérieur du système solaire, la gravité
n'est donc toujours pas "la" loi.
| I
accueil |
E
Science |
G
haut |
|
O
auteur
|
 selon
notre hypothèse, 3 neutrinos en boucle fermée triangulaire
= 1 quark up (l'une des "briques" du noyau des atomes)
selon
notre hypothèse, 3 neutrinos en boucle fermée triangulaire
= 1 quark up (l'une des "briques" du noyau des atomes) 2
quarks up triangulaires et 1 quark down en va-et-vient forment ensemble
une structure tridimensionnelle : le proton d'un atome de matière
2
quarks up triangulaires et 1 quark down en va-et-vient forment ensemble
une structure tridimensionnelle : le proton d'un atome de matière  un
atome d'hélium 4, formé de 2 protons et de 2 neutrons tête-bêches,
un
atome d'hélium 4, formé de 2 protons et de 2 neutrons tête-bêches,