Peirce décrit les icônes-diagrammes comme "celles qui représentent les relations, principalement dyadiques ou considérées comme telles, des parties d'une chose par des relations analogues dans leurs propres parties", ce qui est rigoureusement équivalent à notre définition.
Nous avons déjà donné un exemple d'icônes-diagrammes : celui du système nerveux de la grenouille qui est un sinsigne iconique lorsqu'il est produit par un élève, un légisigne iconique dans son manuel de biologie. Les qualités en question sont des qualités graphiques ; le dessin est décomposable en traits (courbes, segments et droites) qui mis bout à bout de façon convenable constituent le diagramme et mettre deux traits bout à bout c'est constituer une relation dyadique entre les qualités de chacun de ces traits. On peut citer des icônes-diagrammes sonores comme tout ce qui en musique évoque des choses réelles (par exemple, "Pacific 231" d'Arthur Honegger) et les enfants en produisent continuellement dans leurs jeux (le pistolet, mais aussi la moto imaginaire qu'ils imitent en produisant simultanément des icônes-diagrammes sonores et visuelles). L'icône-diagramme gustative est illustrée par cette anecdote selon laquelle un dégustateur professionnel identifia une clé avec son porte-clés en cuir tombés dans un tonneau à partir d'un goût de fer et de cuir.
Il est un genre d'icône-diagramme qu'on appelle icône logique qui joue un rôle fondamental dans les sciences formelles et par voie de conséquence dans les sciences formalisées. Toute formule de la physique, toute formule chimique en est un exemple. Soit la formule exprimant la loi d'Ohm U = RI ; elle montre que les mesures de trois grandeurs (représentées par les symboles rhématiques U pour la différence de potentiel, R pour la résistance et I pour l'intensité du courant) sont liées par deux relations dyadiques __ x __ (multiplication) et __ = __ (égalité) de la façon suivante __ = (__ x __). La formule dévéloppée du méthane par exemple
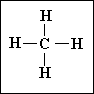
est un exemple encore plus frappant.
Mais c'est peut-être en algèbre qu'on trouve les meilleures illustrations quant à l'intérêt de cette catégorie d'icônes pour la compréhension de l'activité mathématique. Soit un système très classique de deux équations à deux inconnues :
ax + by = c
a'x + b'y = c' (avec ab' - a'b différent de 0)
il montre que les grandeurs symboliquement représentées par les lettres x et y sont dans deux relations dyadiques (a_ + b_) = _ d'une part et (a'_ + b'_) = _ d'autre part. Résoudre le système c'est montrer que ces prémisses sont équivalentes à la conclusion selon laquelle ces mêmes grandeurs sont dans les relations monadiques _ = xo ; _ = yo par une suite d'arguments déductifs qui assurent la vérité de cette conclusion. Résoudre ce système c'est donc opérer sur la configuration des relations de façon à faire ressortir ce qui est implicite dans les données, c'est-à-dire à montrer que x = xo et y = yo.
Les figures de géométrie sont, de toute évidence, des icônes-diagrammes (légisignes) et chercher un problème de géométrie c'est expérimenter sur des répliques de légisignes de façon à déduire d'une configuration de départ la vérité de la configuration demandée qui constitue la question du problème.
![]() Retour à l'index de la zone rouge.
Retour à l'index de la zone rouge.
![]() Parcours conseillé
Parcours conseillé