home
contents Mathematics
how to travel from one number toward another?
the difference between fractal and space dimensions
home |
contents Mathematics |
previous
: how to travel from one number toward another? |
next
: the difference between fractal and space dimensions |
| direct to all other pages of the section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
Mandelbrot fractal dimensions to the rescue
After this wide detour to learn how
to calculate decimal values correctly, we go back to curved deformations.
We left them [to
see again ![]() this moment] saying that in a single point we wanted to represent
the whole set of solicitations which tend to make that point move in space.
And we have acknowledged then that these solicitations have to be represented
by an infinite number of vectors, each of these vectors having a specific
intensity, and each being oriented in a specific direction of space.
this moment] saying that in a single point we wanted to represent
the whole set of solicitations which tend to make that point move in space.
And we have acknowledged then that these solicitations have to be represented
by an infinite number of vectors, each of these vectors having a specific
intensity, and each being oriented in a specific direction of space.
To represent the whole set of vectors
which compel the body to move, we
must have at our disposal 3 distinct types of data:
1/
first, we have to indicate that what occurs to the physical body, is a
deformation of its position, that is, a move in space. It could have been
a different type of deformation. For example, it could have been a deformation
which pierces it, or stretches it, or inflates it, or compresses it.
2/
then, we have to indicate the intensity of the deformation of its position.
3/
at last, we have to know how this intensity varies, along with all the
directions of space.
Now, it happens that our analysis
of the generation of whole and decimal numbers, shows us that a
fractional number necessarily holds 3 types of distinct data:
1/
the first concerns the whole number it is linked to.
2/
the second concerns the sequential ordering of the deformations made to
the unit.
3/
the last, concerns the value of this deformation for each of the decimal
sequences.
| So, this suggests a simple way to
measure the dimension of curved deformation to which a point is subjected:
we only have to use an irrational number whose whole part would
tell the type of deformation, and its decimal part -- whose length is infinite
-- would tell how the intensity of the deformation varies for every
of the infinite number of space directions.
At this point, we remember the
fractal dimensions of Mandelbrot.
|
First, we consider the whole digit they
bear before the decimal point.
- 0 -
we began introducing deformation dimensions with the
deformations of a contrast,
such as a 'Cantor dust': that is a bar whose central 1/3 is removed, whose
central 1/3 of the 2 remaining segments is removed, and so on, to infinity
[to see ![]() that figure again]. It happens that the fractal dimension of
such a Cantor-dust, where the deformation implies no displacement, is Log
3/ Log 2, that is about .63.
that figure again]. It happens that the fractal dimension of
such a Cantor-dust, where the deformation implies no displacement, is Log
3/ Log 2, that is about .63.
Then,
its whole part is 0.
- 1 -
as we shall see in the next examples [images below] the
fractal values of the paths
that Mandelbrot gives in his book 'The Fractal Geometry of Nature', all
have values between 1 and 2. That is to say that their
whole part is always 1.
- 2 -
at last, the fractal value of a 'Peano curve', which deforms the pavement
of a surface on itself, is 2 [see this figure ![]() in the next page]. The basis of that figure is to regularly
change the distribution of white part and black part on a sheet without
changing their mutual proportion: every time, it makes a more tortuous
division between the 2 surfaces.
in the next page]. The basis of that figure is to regularly
change the distribution of white part and black part on a sheet without
changing their mutual proportion: every time, it makes a more tortuous
division between the 2 surfaces.
Then, the
whole value 2, in a fractal dimension, may have to do with the
deformation of a body on itself.
Now, the decimal value of fractal dimensions:
we know that most of the time it's an irrational number, resulting from
the division of 2 logarithms. Then, it does hold infinity of sequenced
deformations.
What remains to be seen, is the graph representation
of that dimension.
[the images are from the french
translation of the book of Benoit Mandelbrot: 'Les Objets Fractals' - Flammarion
publisher]
For example, Mandelbrot gives the
fractal dimension Log 4/ Log 3, that is roughly 1.2618, for the Von Koch
'snowflake curve'. This curve cannot really be drawn, for it corresponds
to an infinite process: we begin with an equilateral triangle, on every
side of the triangle, we make an equilateral triangle on its central 1/3,
on every side of the last triangles we made, we make an equilateral triangle
on their central 1/3, and so on, . . . till infinity.
 |
generation
of the Von Kock 'snowflake curve'
(to go on till infinity) |
 |
the Von Kock
'snowflake curve'
Dimension = Log 34 ~ 1,2318 |
| Another example: for a fractal dimension value Log 5 / Log 4, that is roughly 1.16, we get this kind of curve, which we also have to carry on to infinity. Here, only the first 2 steps are represented. | 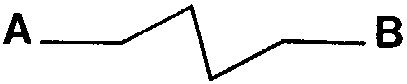 |
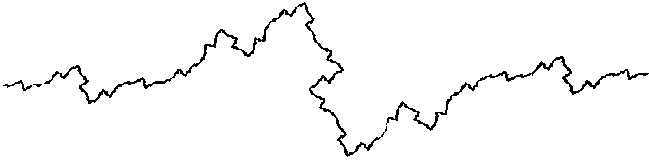 |
Dimension = Log 45 ~ 1,16 |
We immediately notice the graph significance,
of the correspondence between fractal dimensions and such curves.
To represent the value of a force
of a vectorial type, a vector precisely was enough.
A fractal curve is not far from
having the same simplicity as a vector, for we needn't represent the whole
infinite curve. As
we find the same curve on all scales, and the same details in all details,
we have no need to bother drawing it all. One only scale is enough.
And we have better use the bigger one. Thus, in the case of the dimension
'roughly 1.16', the diagram AB is enough to virtually represent the infinite
number of curves which are made on the same model, on all possible scales.
Nevertheless, a question remains:
in the same way as we can graphically calculate the combination of several
vectorial forces by using their resultant vectors, can we hope to calculate
graphically the combination of several curved deformations with any construction
made on their fractal curves?
We shall make no suggestion here
about this issue which will remain open.
How to
find a fixed value, for the fractal dimension of a path
Now, if we consider the curve AB
in the above drawing, not as a drawn figure, but as the path of a body
moving from A to B, we say to ourselves that this type of path calls well
enough to mind what occurs when a body is driven toward another by a curved
deformation: the graph shows that it starts from A, arrives in B, and that
to make this path it isn't subjected to an attraction directed toward B
only, but also toward other directions.
In short, it ends up arriving in
B and not missing it, only because these attractions, according to all
different directions, are well combined together. And this, on all scales
of the path.
Nevertheless, there is a major objection,
made by Mandelbrot himself, concerning the use of fractal curves as the
valid representation of a path followed by a moving body. This objection
concerns the length of the path.
In fact, if we calculate the length
of a fractal curve, we notice it can be infinite. Every time we go down
one notch in the scale details of its path, we turn a straight segment
into a series of segments that undulate on this 1st segment. As a straight
line is the shortest way between 2 points, therefore every step in the
'refinement of detail' has for consequence to lengthen the curve. Some
infinite suites converge to a finite sum, but not in this case, for the
lengthening factor of the path does not decrease with the scale of details.
Thus, if the curve is of infinite
length, we cannot use it to measure the path of a body, which will be,
for its part, perfectly finite.
We can also decide not to draw the
curve in all its infinite details, in order to have a fixed result. But
in this case, according to the scale used to measure the path, that is
according to the degree of details used, the length of the path will not
be the same every time.
| So, a fractal path has an infinite
length, or has a variable length according to the scale of its measurement.
Therefore, we start off pretty badly when using a fractal curve to represent
the path of a body driven by a curved deformation.
On this point again, the analysis we have made on decimal numbers, will be useful to understand where the anomaly comes from. |
| In a system
of measurement with coordinates, a path has only one possible length.
In a system of measurement with deformation dimensions, a path has an infinite number of possible lengths, that are summaries in one number only. Then, a fractal dimension is infinitely bigger in data than a coordinate dimension. It only asks, which of the paths we are to take, before giving us its length. |
home |
Math |
top |
next
: |
author |