home

contents Mathematics

previous :     the difference between fractal and space dimensions

next :    Ian Stewart drips his tap

Continuity of deformations in space
 

A continuous path is a path which does not make sudden jumps. So to speak, every position 'touches' the following one. The body does not disappear from a place to reappear in a far away place at the closest following instant.
By analogy with a continuous path, a continuous deformation doesn't make a sudden break between two contiguous states. It may break sometime, but then, it's really broken and the deformation has come to an end.
 

When 2 bodies are not linked continuously in space, we state they are separated. We state that they do not constitute any more one body which deforms itself in space, but constitute two distinct bodies. That's the precise point we shall consider is wrong. Comment:  here we shall limit ourselves to evoke discontinuous phenomena 'on the usual scale of visibility'. But the reasoning will be worth all the way for the area of elementary particles, where the same type of questioning is more and more frequent, in terms of: 'how can 2 particles, which are too distant to have enough time to exchange data at the speed of light, react in a coordinate way so that what happens to one, interacts instantly to the other?'

We begin with a visibly continuous deformation.
We take a receptacle in which we have water rotating. Then in the swirl, we drop an ink drop. We can perfectly see how the drop deforms itself. That is, dilutes itself, and begins moving driven by the water. The continuity of this deformation, implies for example that colored water will not appear all of a sudden in any volume of clear water. Colored water appears only in places where the movement can drive some ink, or in places where the dilution by diffusion has brought some.
 

Now we make another experiment.
[in 'l'ordre du chaos' - 'la mémoire des atomes', by Richard Brewer and Erwin Hahn - Bibliothèque Pour la Science - diffusion Belin. The photographs of this experiment are from this article, and in order from left to right on the first line then on the second line]

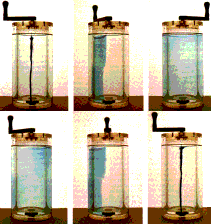Inside a fixed cylinder we place a rotating one, and the space between the two cylinders is filled with a transparent and viscous fluid. We let a vertical dribble of coloring leak. Then we rotate the inner cylinder till the coloring is mixed with fluid.
At this point, all is 'normal', in a continuous way. Exactly as in the first experiment, except that viscosity doesn't add an effect of diffusion to the effect of mixing by movement.

When the coloring is mixed, we start rotating the cylinder in the opposite direction. Little by little the coloring 'demixes', and after an equal number of tours the vertical dribble of coloring is perfectly restored. That's a bit amazing. Even more so for someone who can only see the 2nd part of that experiment: in front of him he has a liquid in which a coloring is being mixed, he rotates it, and instead of mixing a little more as it usually does, it 'demixes'.

Astonishing as it may be, it remains continuous. The coloring does not reappear demixed suddenly, at random in the liquid. It 'reconcentrates' in a continuous way.
 
 

Usually it is said that this experiment reveals 'the hidden order of chaos', and the authors of the article where this experiment is related see in it an aspect of 'atoms memory'. Here will the hypothesis be that, in fact, there is no real 'chaos' when the coloring is dispersed, for precisely we suppose that the coloring molecules never really disperse. They never completely lose their respective positions, and therefore they do not find them again in the end, 'as if by magic'. Such a perfect restoration of initial arrangement, after a complete dispersion, seems to us, unlikely. It can only occur if the arrangement never really dismantles. That is to say that in the dilute and medium phase of the experiment, the molecules of coloring that we see separated in space, each on opposite sides of the cylinder, are in reality, that is, in the phenomenon reality, always as if side by side, as if linked continuously the ones with the others. Exactly as they are at the beginning of the experiment, and at its end.

 

Molecules cannot have their initial position 'in memory' for they have no memory organ, and so they cannot 'find again' their initial position at the end of the experiment. They always remain in it by some aspect of the phenomenon.
What this aspect of the phenomenon is, we can now tell: it's a dimension. The positions of the molecules are continuous in a dimension of the phenomenon. For us, the problem is that space dimensions do not show this dimension.
And they do not show this dimension because they cannot do it, which is what we shall try to explain now.

With this aim, we shall face in our turn the eternal and irritating problem of the dripping tap.
 
 

home

Math

top

next :       Ian Stewart drips his tap

author