home
contents Mathematics
continuity of deformations in space
birh of a dimension
home |
contents Mathematics |
previous
: continuity of deformations in space |
next
: birh of a dimension |
| direct to all other pages of the section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
We shall first summarize Ian Stewart's
narrative [Does God play Dice - § Plumbing the Depths - Penguin
Books] about the onset of chaos in the rhythm of drops dripping from
a tap.
Then, we shall suggest an interpretation
of 'what's happening', and what makes the phenomenon become suddenly chaotic.
| We open a tap just a little bit.
A drop slowly forms, bulges, then detaches itself, and makes 'drip' when
falling in the washbasin. If we listen to the drops dripping the ones after
the others, then we hear 'drip-drip-drip-drip-drip, and so on' (sound effects
are from Ian Stewart. His translator in French, hears: floc-floc-floc).
We open up the tap a little more, and drops begin by joining in pairs: two drops very close, then a longer interval, then two close drops again. Ian Stewart hears: 'dripdrop-dripdrop-dripdrop'. His translator hears 'flicfloc-flicfloc-flicfloc'. We open more. The rhythm of the dripdrop speeds up. The more we open, the more the gap between a drip and a drop decreases, and the more the gap between a dripdrop and another dripdrop decreases. We open a little more, just a tiny more, and all of a sudden, with no visible cause, the rhythm of the falling drops becomes completely irregular, without any periodicity, completely chaotic. |
The thing
was experimentally measured.
Ian Stewart mentions this in the same book, in 'Bashô Revisited'.
Robert Shaw and colleagues at the
University of California, Santa Cruz, began by measuring roughly 5,000
time intervals between successive drips, in the chaotic phase of a dripping
tap. Their rhythm did have a random aspect where no regularity could be
found.
Then, they realized what Ian Stewart
calls a 'fake', consisting in building a 3 D figure from the purely linear
series of time intervals. A 3 D from 1 D.
The fake is as follows: we use the
value of a time interval as a 1st coordinate of a point in space. The 2nd
coordinate of the same point is the value of the following time interval
in the series. And its 3rd coordinate is the value of the time interval
which follows again. Then the value used as a 2nd coordinate is now the
first coordinate of a new point, and so on. This fake, changing an 1 D
series in a 3 D figure, is a method settled by Ruelle, Packard and Takens.
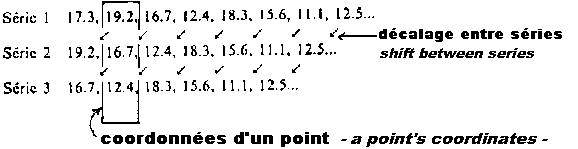
the 'fake'
which transforms a linear series in a 3 D figure,
by successive
shifts
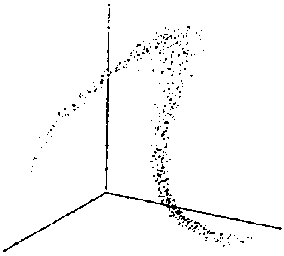 Strangely,
in the case of chaotic intervals between drips, all
the points obtained by handling an apparently random and irregular series
build up together a well-formed figure in space. Strangely,
in the case of chaotic intervals between drips, all
the points obtained by handling an apparently random and irregular series
build up together a well-formed figure in space.
They all stand within the surface of the figure we reproduce opposite. |
Strangely is the word, for we
precisely call that type of figure, 'strange attractor'.
Attractor,
for all points are attracted there.
Strange
for they don't form a 'continuous in time' figure. For instance, if a point
goes to a part of the figure, we absolutely cannot guess whether the next
will be very close to it, or far away, in another end of the figure. It
will be anywhere, but always within the volume of the figure.
| We started with a continuous 1 D
time-series, since time intervals are ordered in the exact order in which
they happened continuously in time, one after the other.
The figure we form has gained several dimensions, but in 'return', it has lost all continuity in time dimension. What happened then? To guess what happened, we shall now reinterpret all the drips dynamic, in terms of deformations. |
A drop which forms can be seen as
the result of the combination of 3 deformations, independent of each other,
in their causes and in their evolution.
-
the 1st cause of deformation is water pressure. The water which
comes from 'behind' pushes the water which is already at the rim of the
tap, and forces it to fall.
-
the 2nd cause of drop deformation is gravity: it hollows the liquid
surface and deforms it.
-
the 3rd cause of deformation is capillary tension that creates a
tension at the surface of the drop, holds back the water, and prevents
it from falling in spite of the water pushing 'from behind', and in spite
of the gravity that attracts it 'from below'.
| [note: in the book 'L'adieu au big-bang' - A farewell to big-bang - from which this text is translated, we see that the entire universe works with a system of dimensions we call 'the dimensions according to universe'. The fist three of these 'dimensions according to universe' works similarly to the three causes of deformation we have just mentioned: the 1st one indefinitely makes restarting, the 2nd one segments, and the 3rd one groups] |
When we start by opening up the tap very slightly,
the combination of these 3 deformations is easy to follow:
- the pressure pushes the water to the tap
exit,
- gravity hollows the surface,
- capillary tension holds it back inside the
tap rim,
and when the weight in the drop is bigger than what this tension can
hold, then the drop gets loose and falls.
It makes a 'drip'.
And it makes room for the following drop that will soon begin to form.
We are in the 'drip-drip-drip' phase.
When we open the tap just a little more,
we shall not leave a drop enough time to quietly form itself alone: the
following drop will begin to form before the previous one has fallen.
Therefore, the following will speed up the fall of the previous one,
and will be itself carried away in that fall.
This is what will group drops in pairs. That's
why we can now hear: 'dripdrop-dripdrop-dripdrop'.
If we still increase the rhythm of the supply
of water, that is, of the 1st deformation, every couple will have
less and less time to form.
Finally, every couple will interfere with the following couple. Then,
every 'pair of couples' with the following 'pair of couples', and so on.
So, rhythm speeds up periodically.
And
all of a sudden, chaos.
The 3 described deformations, have
to do with what we have called 'curved deformations', [to
see ![]() again] for their values vary periodically:
again] for their values vary periodically:
-
water pressure that forces the drop to bulge, passes by a maximum
that we can qualify '1', and is equivalent to a restarting at 0 when the
released drop falls from the tap.
-
it's the same thing for the gravity that applies on a volume of
water (the one of a drop) that increases up to a maximum, then decreases
to 0 when the drop has fallen.
-
it's the same thing again for capillary tension, that regularly
varies with the form of the drop, and regularly tightens more then tightens
less.
In other respects, these
3 curved deformations are incommensurable with each other:
there is no strict relation between what changes water pressure (our hand
turning the tap), what makes the capillary intensity varying (the state
of the shape taken by the drop), and what makes the volume of water affected
by gravity varying coherently and continuously (the inner viscosity of
the liquid).
In spite
of this incommensurability, the added effect of these 3 causes of deformation,
is first 'continuous' in space-time:
we can see clearly every drop appear, bulge, and fall.
It's without surprise.
When we increase pressure and force the 3 causes to interfere the ones with the others, not giving a drop the time to fall before provoking the appearance of another, it's always continuous. Although it's a bit more complicated, we can always guess what will happen, how the rhythm will transform itself.
Then,
when interference reaches a particular point, suddenly it's no longer
continuous in space-time,
for we cannot deduce what will happen now and later, from what has already
happened in space: will the next interval between two drops be shorter
than the previous one? Will it be longer? Will it be the same?
We cannot answer, for there
is no more continuity in the rhythm.
home |
Math |
top |
next
: |
author |