Etude de notre toile
:
Nous avons mesuré chaque rayon de notre spirale
tous les 45° et nous avons disposé ces valeurs
dans le tableau suivant:
| rayon1 |
|
16,9 |
32,8 |
45,2 |
57,6 |
69,9 |
82,7 |
| rayon2 |
12,8 |
17,1 |
33 |
45,8 |
57,4 |
69,7 |
80,9 |
| rayon3 |
14 |
20,1 |
32,3 |
44 |
57,3 |
68,7 |
79,4 |
| rayon4 |
12,6 |
23,5 |
34 |
44,6 |
55,8 |
68 |
79,3 |
| rayon5 |
12,7 |
25,5 |
36,7 |
47,6 |
58,6 |
72,5 |
84,7 |
| rayon6 |
15,5 |
26,5 |
37,5 |
49,6 |
62,9 |
74,6 |
86,8 |
| rayon7 |
15,5 |
27,3 |
38,4 |
50,6 |
64,5 |
76,5 |
86,1 |
| rayon8 |
16,6 |
30,4 |
42,5 |
55,3 |
68,1 |
80,8 |
|
on obtient à partir de ces valeurs le graphique
suivant:
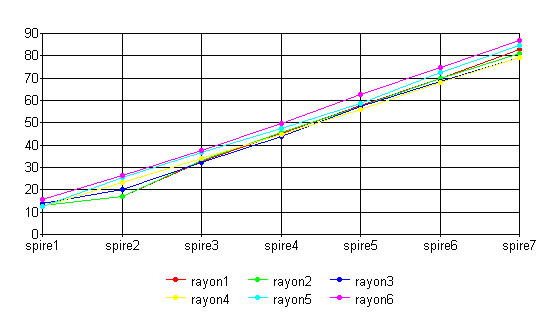
Ce graphique semble d'ailleurs indiquer que chaque
rayon suit une progression arithmétique entre
chaque spire : les courbes représentant pour
chaque rayon la longueur de celui-ci en fonction de
la spire s'apparentent à des droites.
Puis nous avons calculé pour chaque rayon la
distance entre les spires et introduit nos résultats
dans un second tableau :
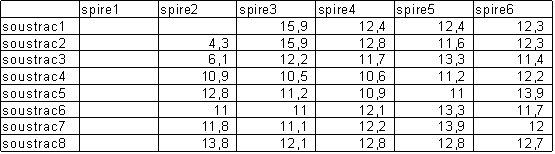
nous pouvons ainsi remarquer que certaines valeurs
sont très proches , ce qui nous incite à
calculer leur moyenne : M1=12,05
Et nous avons enfin calculé, pour chaque point
précédemment répertorié,
le rapport de la longueur du rayon par la mesure de
l'angle , ce qui nous a encore permis d'établir
un tableau de valeurs :
.
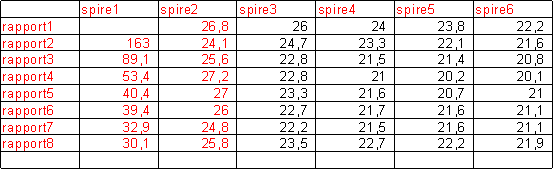
Ce tableau est illustré par ce graphique :
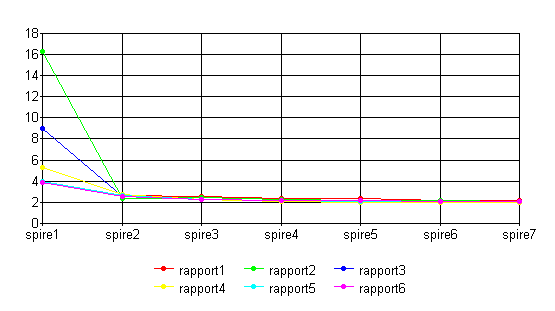
Le tableau et le graphique nous montrent que la plupart
de ces rapports tendent vers une valeur commune. Nous
allons donc calculer la moyenne de tous ces rapports
en excluant toutefois les valeurs obtenues pour les
deux premières spires(en rouge dans le tableau)
:
M2=2,19
D'après le 1, nous déduisons avec la
valeur M2 que si notre spirale est une spirale d'Archimède,
le "a" cherché serait environ égal
à 2,19, alors qu'avec M1 celui-ci serait plutôt
égal à 1,92 (12.05/2/Pi). Cette différence
étant due aux approximations faites pour obtenir
le tableau3.
Nous pouvons donc tracer deux spirales d'Archimède
correspondant le plus possible à notre toile
: l'une définie par a1 et l'autre par a2 :
On tape la ligne suivante dans maple:
plot((2.19*theta/12,theta=0.57..13.54*Pi),coords=polar);
D'où la courbe suivante:
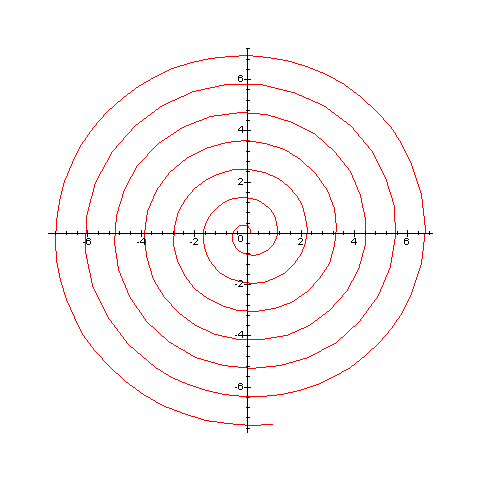
On peut tenter de superposer la courbe obtenue et la
spirale contenue dans la toile:
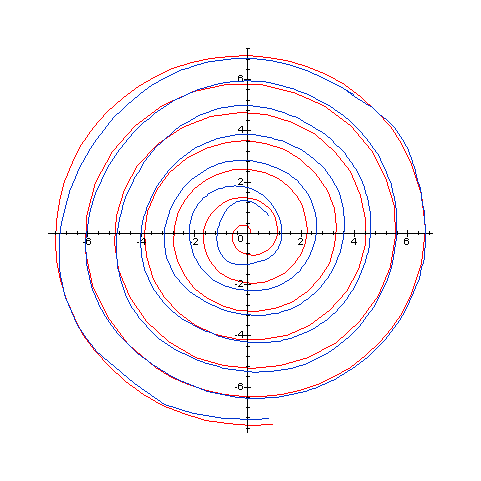
On déduit de tout cela que vers son centre,
la toile ne se rapproche pas d'une spirale d'Archimède
contrairement à sa partie excentrée qui
y parvient avec toutefois une inexactitude relative.
On obtient la modélisation partielle suivante:

Si on complète avec la spirale
que nous n'avons pas étudié,on obtient
la modélisation suivante:

Le résultat obtenu est très
satisfaisant,la spirale la plus adaptée à
la modélisation de la toile semble être
la spirale d'archimède.Elle ressemble assez à
notre toile de départ qui qui étaitla
photo suivante:


|