On place la spirale dans un
repère de centre O.
Observations:
L'écart entre les spires augmente lorsque l'angle
augmente
Les rayons semblent se rejoindrent un même point.
On peut penser à priori que cette spirale est
une spirale logarithmique.
Comment le prouver ?
Cette Courbe a été étudiée
par Descartes et Toricelli en 1638, puis par Jacques
Bernoulli (1654-1705).
On l’appelle également spirale équiangle,
spirale de Bernoulli, spira mirabilis.
Jacques Bernoulli a fait graver une spirale logarithmique
sur sa tombe dans la cathédrale de Bâle,
avec l’épigraphe : eadem mutata resurgo, "déplacée
(mutata), je réapparais (resurgo) à l'identique
(eadem)". Cependant, le graveur a tracé
une spirale d'Archimède...
Une spirale logarithmique a pour équation en
coordonnées polaires
(si l’on considère que le centre de la spirale
est le centre du repère):

avec a différent de 0 et k constant
Exemple de spirale logarithmique:
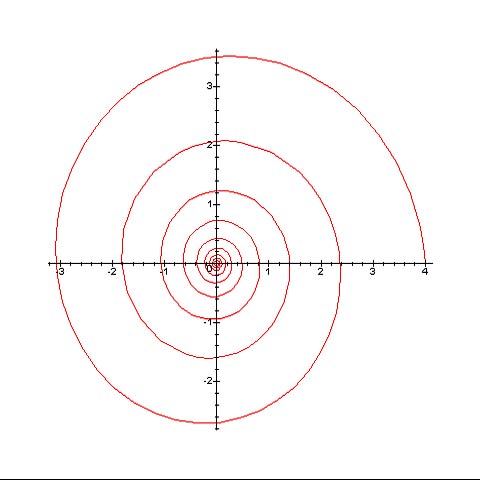
Grâce au logiciel maple on modélise la
spirale logarithmique d’équation :

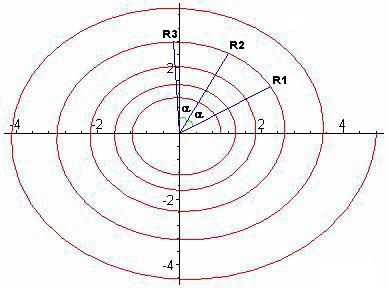
Les quotients des longueurs de rayons de la courbe séparés
par un même angle sont une constante et ne dépendent
que de l'angle.
C'est une propriété nécessaire
pour obtenir une spirale logarithmique.
Pour un écart angulaire a donné : R2/R1
= R3/R2 = constante.
Démonstration:
On prend un point A de coordonnées:
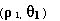
et un point B de coordonnées:
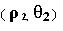
Pour que ces 2 points appartiennent à la courbe,ceux-ci
vérifient nécessairement les relations
suivantes :
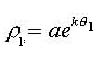
et
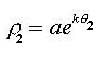
On calcule le rapport suivant :
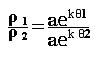
D’où,après simplification par a:
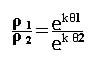
ainsi on obtient :

Puis après factorisation:
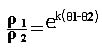
Ainsi le rapport rayon1 sur rayon2(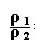 )ne dépend que de leur écart angulaire.Si
l’on prend un écart angulaire
)ne dépend que de leur écart angulaire.Si
l’on prend un écart angulaire  constant,
alors le rapport entre les 2 rayons vecteurs associés
est constant. constant,
alors le rapport entre les 2 rayons vecteurs associés
est constant.
Remarque1 : si 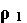 est
supérieur à est
supérieur à 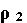 alors alors
 est supérieur à 0 et
est supérieur à 0 et 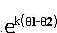 est supérieur à 1(dans le cas contraire
est supérieur à 1(dans le cas contraire
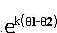 est inférieur à 1).Il en va évidemment
de même avec
est inférieur à 1).Il en va évidemment
de même avec 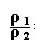 . .
Remarque2 :
Ceci est une condition nécessaire pour qu'une
spirale soit une spirale d'Archimède.Mais est-elle
suffisante la réponse est oui.
démonstration

|

