 accueil accueil
|
|
|
catalogue des effets plastiques
: 
|
7
sur la consolidation des paradoxes
Début 2005, la numérotation des effets plastiques a été complètement modifiée.
Ce texte expose les réflexions qui sont à la base de cette
nouvelle numération, et, bien entendu, il ne s'agissait pas que d'un
problème de numéro. Ce qui est au coeur de cette réflexion,
c'est : comment pouvons-nous supporter en nous un effet paradoxal, et comment
pouvons-nous le saisir, l'apercevoir, l'isoler ?
1- un effet paradoxal a besoin de s'appuyer sur un autre :
En matière de "logique logique", notre esprit est ainsi fait qu'il
ne peut jamais partir de rien, et qu'il doit toujours s'appuyer sur des acquis
logiques précédents.
Ainsi, lorsque nous déclarons qu'une chose est vraie ou qu'elle est
fausse, nous nous appuyons, sans même y penser, sur le principe que
les choses peuvent se classer en choses vraies et en choses fausses. L'existence
du vrai et du faux, en tant que notions séparées, est un acquis
sur lequel nous devons nous appuyer pour pouvoir déclarer, par exemple,
qu'il est vrai que la terre tourne autour du soleil.
Il en va de même pour la "logique paradoxale".
Un paradoxe contient et fait tenir ensemble deux notions qui sont le contraire
l'une de l'autre. Par exemple, dans le paradoxe "continu / coupé",
c'est à la fois continu et coupé, donc à la fois continu
et non continu. Mais notre esprit est ainsi fait que, comme on l'a déjà
dit, pour nous une chose est vraie ou elle est fausse, elle ne peut pas être
les deux à la fois : c'est vrai que c'est continu, ou c'est faux,
c'est-à-dire coupé. C'est l'un ou c'est l'autre, c'est un automatisme
qui fonctionne en nous.
Il y a cependant un biais que peut prendre notre esprit, lorsqu'il doit traiter
de réalités qui sont, qu'il le veuille ou non, de nature paradoxale
: il peut ramener cette contradiction intenable à une autre contradiction
qu'il a déjà admise, ou tout du moins dont le caractère
intenable ne va pas le soucier sur le moment.
Pour reprendre l'exemple précédent, si l'on accepte de considérer
que la terre et le soleil forment deux corps séparés, et que,
par ailleurs, on considère aussi qu'ils forment un couple de corps
liés ensemble par la gravité, alors on considère implicitement
pour acquis et ne posant pas de problème, qu'une chose puisse être
à la fois une et multiple, puisqu'il s'agit ici de "un" couple fait
de "deux" corps séparés.
Si le paradoxe "un / multiple" est donc acquis, c'est-à-dire s'il
ne fait pas problème momentanément d'accepter qu'une chose
soit en même temps une et multiple, alors, pour supporter le "continu
/ coupé" qui nous apparaît intenable, il suffit de considérer
que le "continu / coupé" n'est rien d'autre qu'une forme spéciale de "un / multiple" : si une forme
est continue, c'est qu'elle ne comprend qu'un seul morceau, et si elle est
coupée, elle en comporte nécessairement plusieurs.
_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _
Cette ligne de tirets, par exemple, est ainsi pour nous, et sans problème
apparent, "une" ligne faite de multiples tirets, c'est-à-dire que nous considérons que
la continuité de l'alignement de la ligne est acquise, même si
elle est constamment brisée et contredite par les coupures béantes
qui détachent les tirets les uns des autres.
Ainsi donc,
on peut apprivoiser le "continu / coupé", s'il nous semble impossible
à concevoir, en s'appuyant sur un autre paradoxe apparemment "non
paradoxal", dans cet exemple, le "un / multiple".
2- comment faire tenir un paradoxe sur un autre :
Bien entendu, le "un / multiple" n'est pas moins illogique que le "continu
/ coupé". Dans les faits, si, à certains moments, il nous semble
supportable de considérer qu'une chose puisse être simultanément
une et multiple, c'est que, sans même nous en apercevoir, nous avons
intégré dans notre esprit l'existence d'un autre paradoxe qui
nous sert à faire tenir ensemble le un et le multiple.
Cela peut être, par exemple, le "intérieur / extérieur"
: la terre est extérieure au soleil, mais elle est à l'intérieur
du couple qu'ils forment ensemble. Autre exemple, pour en revenir à
la ligne continue faite de tirets séparés : lorsque nous considérons
que nous avons toujours affaire à une même ligne continue malgré
ses coupures, c'est que nous admettons que l'extérieur
soit à l'intérieur, en l'occurrence que l'extérieur de
chaque tiret soit à l'intérieur de la ligne continue qu'ils
forment ensemble.
Cela peut être aussi le "lié / indépendant" : la terre
et le soleil sont deux corps indépendants, mais ils sont liés
par l'effet de gravité. Dans le cas de la ligne de tirets, nous considérons
que les tirets qui sont complètement indépendants
les uns des autres, sans aucun point commun ni rien qui les attache, sont liés à un même alignement dont
ils ne s'écartent pas et qui les lie donc ensemble très fermement.
La "logique logique", pour faire tenir en nous des développements
logiques, utilise un procédé spécifique : elle déroule
et combine les propositions logiques les unes après les autres. Puisque
ceci, et puisque cela, alors on peut conclure telle chose, et puisque par
ailleurs on a aussi telle autre chose, cela entraîne telle autre chose
encore, etc. etc.
La "logique paradoxale", pour faire tenir
un paradoxe en nous, se développe elle aussi selon un procédé qui lui est spécifique et que
l'on peut précisément décrire.
En fait, ce procédé est déjà décrit ailleurs
dans le site, puisqu'il n'est autre que le procédé qu'utilise
toute complexité pour se consolider en 4 stades successifs de complexité
croissante : 0 - le stade des points séparés, 1- le stade du classement,
2- le stade de l'organisation, puis enfin 3- le stade du nouage qui stabilise définitivement
une réalité dans le temps [voir le texte qui les présente].
C'est de la même façon, en effet, qu'un paradoxe va pouvoir tenir en nous.
L'exemple de la ligne de tirets va nous servir à nouveau, pour comprendre
comment 4 paradoxes nous sont en fait utiles pour nous permettre de supporter
que le continu puisse être coupé sans rien renier de sa continuité.
Cet exemple correspond à l'effet paradoxal qui est répertorié a10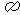 , et, en suivant ce lien, vous pouvez le retrouver dans le répertoire
qui regroupe l'ensemble des effets paradoxaux. Le symbole
, et, en suivant ce lien, vous pouvez le retrouver dans le répertoire
qui regroupe l'ensemble des effets paradoxaux. Le symbole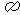 indique que le paradoxe qui a besoin de s'appuyer sur d'autres est ici
le
"continu / coupé", dont ce schéma est le symbole. "a"
signifie analytique, ce qui correspond au fait qu'il nous faut
impérativement choisir de s'arrêter
à la coupure ou de la franchir, et que nous ne pouvons donc pas
lire en même temps la continuité et la coupure [aller au texte qui explique la différence entre un effet analytique et un effet synthétique]. "10" est le numéro du paradoxe "lié /
indépendant", ce qui indique que c'est d'abord sur ce paradoxe que
nous nous appuyons.
indique que le paradoxe qui a besoin de s'appuyer sur d'autres est ici
le
"continu / coupé", dont ce schéma est le symbole. "a"
signifie analytique, ce qui correspond au fait qu'il nous faut
impérativement choisir de s'arrêter
à la coupure ou de la franchir, et que nous ne pouvons donc pas
lire en même temps la continuité et la coupure [aller au texte qui explique la différence entre un effet analytique et un effet synthétique]. "10" est le numéro du paradoxe "lié /
indépendant", ce qui indique que c'est d'abord sur ce paradoxe que
nous nous appuyons.
0- D'abord, donc, pour exprimer et supporter le "continu / coupé", nous nous appuyons "ponctuellement"
sur un autre paradoxe, qui est ici le "lié / indépendant".
"Ponctuellement", cela veut dire : sur celui-ci et pas sur un autre.
Cela veut dire aussi, assimiler les deux paradoxes, les fondre comme deux
points viennent se confondre l'un avec l'autre.
Comme on l'a évoqué précédemment, s'appuyer sur
un autre paradoxe cela signifie que, pour supporter l'impossibilité
qu'une chose soit à la fois continue et coupée, nous la ramenons
à une autre situation paradoxale que, pour l'occasion, nous tenons
pour acquise. Ici, nous ne voyons donc pas de problème à ce que
des tirets soient complètement indépendants les uns des autres,
et qu'ils soient en même temps liés les uns aux autres par leur
commune participation à un même alignement dont ils ne s'écartent
pas.
Si nous supportons ici le paradoxe "lié / indépendant", ce
n'est pas qu'il n'y ait pas de paradoxe à ce que plusieurs choses
soient complètement indépendantes les unes des autres tout
en étant complètement liées les unes aux autres. Nous
le supportons parce que, dans cette configuration visuelle, la notion d'alignement
et la notion d'écartement des tirets les uns des autres nous semblent
assez étrangères l'une de l'autre, et qu'il ne nous vient
donc pas à l'esprit de confronter brutalement ce que cela implique
comme lien et comme indépendance entre les tirets.
Donc, puisque les tirets indépendants sont liés entre eux par
leur participation à un même alignement, nous pouvons nous appuyer
sur cet effet pour lire que ces tirets, pourtant bien coupés visuellement
les uns des autres, forment ensemble un alignement continu. Et nous voilà
ainsi, avec une la ligne dont nous pourrons admettre qu'elle est "continue
/ coupée", c'est-à-dire que nous pourrons la lire comme simultanément
continue et coupée. Plus exactement, et c'est là tout l'intérêt
qu'il y a à dessiner des formes "continues / coupées", nous pourrons
nous appesantir en la voyant sur ce paradoxe qu'elle exhibe, nous pourrons
regarder "droit dans les yeux" cette impossibilité pourtant possible,
nous pourrons l'affronter pour constater, par exemple, que c'est bien notre réalité d'individu
"continu avec les autres / coupé des autres" qui nous pose problème.
1-
Ensuite, il nous faut prendre un autre paradoxe encore. Si l'on a ramené
le "continu / coupé" au "lié / indépendant" pour pouvoir
le supporter, il faut cependant que nous ne confondions pas ces deux paradoxes,
sinon le "continu / coupé" serait complètement rabattu sur
le "lié / indépendant" et il disparaîtrait en tant que
paradoxe distinct. Donc, il nous faut différencier ces deux paradoxes,
c'est-à-dire les "classer",
ressentir qu'ils ne sont pas équivalents comme le sont deux points
confondus, ni même comme deux points séparés. Les différencier
ou les classer, pour en revenir à notre ligne de tirets, cela implique
de ressentir qu'ils n'ont pas exactement la même relation avec cette
ligne.
Si l'on ressent que les tirets indépendants sont liés sur une
même continuité, c'est parce que l'on considère que les
tirets pourraient tout aussi bien avoir des directions différentes
puisqu'ils ne sont pas attachés les uns aux autres, mais qu'ils sacrifient
à la contrainte d'être dans le même alignement :
pas _ / \ _ _ \ mais _ _ _ _ _ _ _ _ _ _
Mais, si l'on ressent que la ligne est simultanément continue et coupée,
ce n'est pas fondamentalement cette notion d'alignement à la queue
leu leu que l'on a en tête, mais c'est plutôt la notion que la
ligne se poursuit, bien qu'elle soit déchirée :
pas _______________ mais _ _ _ _ _ _ _ _ _ _
On avait commencé par ramener le "continu / coupé" au
"lié
/ indépendant", par l'assimiler à lui. Pour maintenant le
différencier du "lié / indépendant" il est utile
de comprendre comment l'essence de la ligne de tirets n'est pas
épuisée
par le "lié / indépendant". Si la même ligne peut
exprimer à la fois
l'effet de "lié / indépendant" et l'effet de "continu /
coupé",
cela veut effectivement dire qu'il y a quelque chose de plus puissant
encore que le
"lié
/ indépendant" dans l'effet que nous procure la ligne de tirets.
Cela
n'a pas besoin d'être beaucoup plus puissant : un cran au-dessus
suffit.
Et cela doit rester compatible avec le caractère paradoxal des
deux
paradoxes déjà envisagés. Paradoxal et un cran
plus puissant que le "lié / indépendant", cela ne peut
être qu'une
chose : le paradoxe qui est un cran plus puissant que le "lié /
indépendant".
Ce paradoxe, ainsi qu'on peut le voir dans le tableau qui les regroupe, c'est le "même / différent".
Ainsi, il y aurait du "même / différent" dans la ligne de tirets
? Oui, évidemment : différents tirets forment ensemble une même ligne.
_ + _ + _ + _ + _ + _ = ( _ _ _ _ _ _ _ _ _ )
On pourrait aussi observer un autre effet de "même /
différent",
en constatant que les différents tirets sont les mêmes,
c'est-à-dire
qu'ils ont la même longueur. Mais c'est parce que l'on a
considéré
jusqu'ici le cas particulier d'une ligne faite de tirets identiques,
or, constatez-le, tout ce que l'on a dit jusqu'ici reste valable si la
ligne est faite
de "différents " tirets qui sont "différents entre eux".
On
oublie donc cet aspect pour ne retenir que le fait que la même
ligne (au sens de
1 seule) regroupe différents tirets (au sens de plusieurs
tirets)
:
___ + __ + _ + ____ + _ = ( ___ __ _ ____ _ )
Revenons-en au rôle tenu ici par le paradoxe "même / différent"
: parce que nous admettons qu'une "même" ligne soit faite de "différents"
morceaux, alors nous pouvons nous concentrer sur le fait que ces différents
morceaux, bien que tous "indépendants" les uns des autres, sont "liés"
par leur appartenance à un alignement commun, et, grâce à
cette constatation, mais par ailleurs, nous pouvons admettre que cette "même"
et unique ligne "continue" soit déchirée en "différents"
morceaux complètement "coupés" les uns des autres.
Admettre que la "même" ligne soit faite de "différents"
morceaux,
nous permet donc de mettre en relation deux aspects de cette
réalité,
d'une part le fait que les morceaux sont liés ensemble sur un
alignement
commun (paradoxe "lié
/ indépendant"), et d'autre part le fait que cette ligne
continue est déchirée (paradoxe "continu /
coupé").
Mettre en relation, cela veut dire séparer ces deux aspects, et,
en
même temps, permettre de faire jouer leurs différences. Ce
qui est donc mis ici en relation par le
"continu / coupé", c'est le "lié
/ indépendant" et le "continu / coupé".
2-
Grâce au "lié / indépendant", on peut donc supporter le
"continu / coupé", et, grâce au "même / différent",
on peut ressentir que ce qu'il y a de "même / différent" dans
chacun des deux premiers paradoxes n'est pas identique et donc qu'il s'agit
bien de paradoxes séparés et différents l'un de l'autre.
Mais si chacun des deux premiers paradoxes peut se ramener à du
"même / différent", une nouvelle confusion pourrait s'instaurer
: qu'ils ne soient rien d'autre que deux aspects du "même / différent".
Pour éviter cette confusion, la solution est d'utiliser
maintenant un autre paradoxe que le "même / différent"
pour classer le "lié / indépendant" et le "continu /
coupé". En somme, nous classons simultanément ces
paradoxes de deux façons différentes, ce qui revient
à "organiser" leurs différences.
La méthode pour cela n'est pas autre pour cela que celle qui
nous a conduit à utiliser le "même /
différent". Il nous faut seulement prendre un nouveau paradoxe
de référence qui soit un cran plus puissant encore que le
"même / différent". Le tableau des 16 paradoxes
nous indique qu'il s'agit du "intérieur / extérieur",
c'est-à-dire que nous considérons maintenant que
l'extérieur de chaque tiret est à l'intérieur de
la ligne :
(___) (__) (_) (____) (_) = ( ___ __ _ ____ _ )
Parce que nous admettons qu'à l'intérieur d'une ligne se
trouve l'extérieur de plusieurs tirets, c'est-à-dire,
parce que l'on y rencontre successivement le début et la fin de
chaque tiret, alors nous pouvons d'une nouvelle façon nous
concentrer sur le fait que ces tirets isolés à
l'intérieur de la ligne, bien que tous "indépendants" les
uns des autres (indépendants car munis de leur propre
début et de leur propre fin, donc de leurs propres
frontières extérieures), sont "liés"
par leur appartenance à un alignement commun (car tous à
l'intérieur d'une même ligne), et, grâce
à
cette constatation, mais par ailleurs, nous pouvons admettre que cette
ligne "continue" soit déchirée à son
intérieur par la présence de ces morceaux, puisque chacun
est muni d'un début et d'une fin, ce qui implique donc que
chacun de ces morceaux est complètement "coupé" des
autres.
Admettre qu'à "l'intérieur" de la ligne on rencontre
successivement "l'extérieur" de plusieurs morceaux de ligne
nous permet donc de mettre en relation deux aspects de cette
réalité,
d'une part le fait que les morceaux sont liés ensemble sur un
alignement
commun (paradoxe "lié / indépendant"), et d'autre part le fait que cette ligne continue est
déchirée (paradoxe "continu / coupé").
Puisque cette mise en relation avait été
déjà possible avec le paradoxe "même /
différent", nous ne craignons pas que cette nouvelle mise en
relation ne soit permise que parce que le "continu / coupé" et
le "lié / indépendant" ne seraient que deux aspects du
"intérieur / extérieur", et, inversement, nous ne craignons
plus que la première mise en relation n'était permise que
parce qu'ils n'étaient que des aspects du "même /
différent".
3-
Nous avons donc appuyé le paradoxe qui nous pose problème
sur un premier paradoxe, puis nous avons pris un second paradoxe pour
les mettre en relation et s'assurer qu'ils n'étaient pas les
mêmes, puis nous avons pris un troisième paradoxe pour les
mettre en relation sous un jour différent. Pour finir, il nous
reste à prendre un quatrième et dernier paradoxe
qui va nous servir à "nouer"
cet appui, c'est-à-dire à empêcher qu'il
ne se défasse lorsque le paradoxe ainsi consolidé sera
confronté à d'autres paradoxes qui chercheront à
tirer vers eux son effet.
Nouer,
cela veut dire que les deux mises en relation successives que l'on a
faites doivent être contenues dans une relation encore plus
forte, relation qui va les relativiser toutes les deux et permettre de
les garder côte à côte, et donc de toujours les
faire jouer simultanément ainsi qu'il est utile.
Pour cela, comme on l'a fait les deux fois précédentes,
on va avoir recours au paradoxe un cran plus élevé encore
que celui qui nous a servi à organiser l'appui. Dans l'exemple
de la ligne de tirets, le paradoxe un cran plus élevé que
le "intérieur / extérieur", c'est le "un / multiple",
c'est-à-dire, et ainsi que nous l'avons déjà
envisagé plus haut, nous allons considérer qu'il y a
à la fois "une" seule ligne et de "multiples" tirets :
(1___) (2__) (3_) (4____) (5_) = ( ___ __1 _ ____ _ )
Nécessairement, puisqu'il est plus puissant que les trois
paradoxes précédents, le "un / multiple" les reprend et
les résume. Ainsi, puisqu'une ligne de tirets contient de
multiples tirets, cela implique que ces tirets "indépendants"
sont "liés" sur un même alignement, cela implique aussi
que la "même" ligne contient "différents" tirets, et cela
implique enfin que "l'extérieur" de chacun des tirets est
à "l'intérieur" de cette ligne.
3- un peu de subtilité :
Ainsi qu'on vient de le voir, lorsque l'on considère un seul
effet paradoxal, on en manie en fait cinq : celui qui nous sert
d'appui, celui qui classe les deux premiers, celui qui organise leur
relation grâce à un second classement, et enfin celui qui
noue l'organisation de l'appui.
Puisque chaque paradoxe peut s'appuyer sur n'importe lequel des 15
autres, chacun des 16 paradoxes peut ainsi apparaître sous 15
facettes différentes, ce qui fait au total 15 x 16 = 240
combinaisons à caractère analytique, et autant à
caractère synthétique, soit 480 au total. Les liens du
tableau des 16 paradoxes mènent aux 16 fiches qui mènent
chacune à l'un de ces 480 effets paradoxaux possibles.
Mais si chacun des paradoxes dispose de 15 appuis possibles, et donc de
15 facettes différentes, ce n'est pas l'une de ces facettes
qu'il va utiliser lorsqu'il sera lui-même utilisé pour
appuyer un autre paradoxe. Dans ce cas, c'est son expression "la plus
pure" qui sera utilisée, et l'on peut même dire que ce
n'est que lorsqu'il sert d'appui à un autre qu'un paradoxe
apparaît dans "toute sa pureté", puisque, lorsqu'il est
lui-même exprimé, il a besoin d'un appui et
n'apparaît alors que sous l'aspect restreint que cet appui met en
valeur.
Dans le chapitre 4- suivant on reviendra sur cette notion, que l'on
veut seulement introduire ici en revenant sur l'exemple de la ligne de
tirets.
Dans cet exemple, cela implique que le paradoxe "lié /
indépendant" qui a servi d'appui au "continu / coupé"
était alors sous sa forme la plus pure, cette forme
consistant à considérer que des
parties qui sont physiquement complètement
séparées appartiennent à un même ensemble.
Ici, nous considérons que les tirets séparés les
uns des autres appartiennent à l'ensemble des traits qui
sont situés dans le même alignement.
Dans le cas des trois autres paradoxes il n'en allait pas de
même, et en toute rigueur il aurait fallu donner une autre
explication pour chacun d'eux. Chacun des trois paradoxes qui
consolident l'appui du premier apparaît en effet sous une forme qui
est "teintée" par le paradoxe qui le suit.
Ainsi, dans le cas du paradoxe "même / différent", si dans
ce cas précis l'explication par les "différents tirets
dans une même ligne" est ici utilisable, elle n'est pas
générale et elle aurait pu ne pas convenir dans un autre
cas de figure. La véritable utilisation qui est faite du
paradoxe "même / différent" lorsqu'il consolide un appui,
c'est : "cela apporte une différence". Ici, cela implique que la
ligne connaît deux types d'endroits qui sont clairement
différents les uns des autres : il y a les tirets, et il y a les
espaces libres de tracé qui séparent les tirets les uns
des autres. L'aspect "différents tirets dans une même
ligne", que l'on peut généraliser par "différentes
fois la même chose pour faire une seule forme", est en fait
l'expression "pure" du paradoxe "même / différent", celle
de ce paradoxe lorsqu'il vient en appui d'un autre paradoxe.
Dans le cas du paradoxe "intérieur / extérieur", on a
évoqué le fait que "l'extérieur des tirets est
à l'intérieur de la ligne", ce qui est une façon
pour ce paradoxe de pencher vers le paradoxe "un / multiple" qui le
suit : il y a de multiples entités à l'intérieur
d'une seule entité globale. Si le paradoxe "intérieur /
extérieur" avait été utilisé en premier
dans l'appui, il aurait eu une expression plus "pure",
c'est-à-dire plus "tordue", où l'on aurait pas
réussi à différencier ce qui fait
l'intérieur et l'extérieur, ainsi par exemple que cela se
passe dans une bande de Möbius. Dans une telle bande, les deux
faces opposées sont à la fois opposées et
continues l'une avec l'autre, de telle sorte que, si l'on
considère une zone de cette bande, on est à la fois
à l'intérieur d'une face à son extérieur.
Cette bande n'aurait pas pu servir en appui d'une ligne "continu /
coupée", mais elle aurait pu servir d'appui pour une surface
"continue / coupée" : continue dans un sens, bien que
coupée en deux faces bien tranchées l'une de l'autre.
Une ligne formant une boucle, par exemple, est une ligne "continue /
coupée" dont l'effet s'appuie sur le paradoxe "intérieur
/
extérieur". La ligne est toujours continue, mais elle est
coupée en trois tronçons dont l'un est d'un
côté de la boucle, l'autre de l'autre côté de
la boucle, et le dernier est constitué de la boucle
elle-même. Dans ce cas, l'espace contenu à
l'intérieur de la boucle, et donc à l'intérieur de
la ligne, est tout entier en dehors du tracé de cette ligne,
donc à son extérieur (nota : si le graphisme ne rend pas
bien continu le O et les traits que j'ai utilisés, faites comme
si !).
_______O_______
Dans le cas du paradoxe "un / multiple", s'il était
arrivé en premier dans l'appui, il y aurait eu une
véritable continuité de la ligne afin qu'elle soit
véritablement une tout en étant multiple. Par exemple,
cela aurait été le cas d'une ligne continue ayant des
tronçons successifs de couleurs différentes : il y aurait
eu une seule ligne, et de multiples tronçons différemment
colorés, et en même temps une ligne à la fois
continue et coupée en tronçons de couleurs
différentes.
_______________________________
Maurice Vlaminck (Les jardins à Chatou - 1904) ou André
Derain (L'Estaque, trois arbres - 1906) utiliseront ce
procédé pour découper des troncs d'arbres continus
en tronçons de différentes couleurs.
Parmi les exemples donnés de l'expression a13 du paradoxe "continu / coupé", expression qui s'appuie
précisément sur le paradoxe "un / multiple", les colonnes
de la Grèce Hellenistique données en référence, ou bien la
femme/bâton de de Dolni Vestonice à l'époque
préhistorique, proposent également des exemples
semblables de lignes continues / coupés, en tablant sur le
changement de texture (lisse / cannelé ou lisse / rayé)
au lieu du changement de couleur.
du paradoxe "continu / coupé", expression qui s'appuie
précisément sur le paradoxe "un / multiple", les colonnes
de la Grèce Hellenistique données en référence, ou bien la
femme/bâton de de Dolni Vestonice à l'époque
préhistorique, proposent également des exemples
semblables de lignes continues / coupés, en tablant sur le
changement de texture (lisse / cannelé ou lisse / rayé)
au lieu du changement de couleur.
Dans le cas du paradoxe "lié / indépendant",
s'il n'avait
pas été en premier dans l'appui, il aurait, lui aussi, eu
une expression différente. Cela aurait correspondu par exemple
au cas d'une ligne munie d'embranchements successifs accrochés
à une partie continue. Dans ce cas la ligne est continue, et
elle est aussi coupée à chacun de ses embranchements qui
s'interrompent et ne continuent donc pas le tracé de la ligne.
Dans ce cas de figure, chaque embranchement est un morceau de ligne
indépendant qui est lié à la partie continue de la
ligne.
____|____|______|______
Avec cet exemple, on veut introduire une deuxième
subtilité qui sera également
généralisée dans le chapitre 4 suivant.
Si le "lié / indépendant" consolide un appui fait
grâce à un autre paradoxe sur le "continu / coupé",
comme ce dernier est situé juste avant le "lié /
indépendant" dans la liste des 16 paradoxes, cela implique que
le paradoxe qui sert d'appui est soit le "rassembler / séparer",
soit le "synchronisé / incommensurable", et que le "continu /
coupé" est en 2e ou 3e position dans cet appui, donc qu'il
intervient dans la consolidation de son propre appui.
Dans
ces cas particuliers, l'intervention du paradoxe qui participe
à sa propre consolidation consiste à forcer les deux
effets contraires à bien se départager sur la forme. Dans
tous les exemples que l'on avait donnés
précédemment, on ne pouvait pas séparer une partie
de ligne continue et une partie de ligne coupée : c'est de la
configuration d'ensemble de la ligne que l'on devait dire qu'elle
était à la fois continue et coupée. Dans l'exemple
ci-dessus, qui correspond an cas où le "lié /
indépendant" ne vient
pas en 1er dans l'appui, on remarque que l'on dispose au contraire
d'une ligne support
qui est fondamentalement continue et de branches qui lui sont
raccordées et qui sont, elles, des lignes coupées.
En l'occurrence, cet exemple correspond à l'expression a7 du "continu / coupé", où le paradoxe "rassembler /
séparer" lui sert d'appui, où le "continu / coupé"
est à la place du paradoxe qui organise son propre appui, et
où le "lié / indépendant" sert à nouer cet
appui. Parmi les exemples que vous trouverez en suivant le lien
ci-dessus correspondant à cette expression, celui de
référence (le cercle des Sarsens de Stonehenge) et les
"Cambell's Soup Can" de Warhol correspondent à l'usage d'une
ligne continue / coupée comme on l'a évoqué avec
le petit schéma ci-dessus.
du "continu / coupé", où le paradoxe "rassembler /
séparer" lui sert d'appui, où le "continu / coupé"
est à la place du paradoxe qui organise son propre appui, et
où le "lié / indépendant" sert à nouer cet
appui. Parmi les exemples que vous trouverez en suivant le lien
ci-dessus correspondant à cette expression, celui de
référence (le cercle des Sarsens de Stonehenge) et les
"Cambell's Soup Can" de Warhol correspondent à l'usage d'une
ligne continue / coupée comme on l'a évoqué avec
le petit schéma ci-dessus.
Après avoir utilisé l'exemple de la ligne continue /
coupée pour introduire les deux subtilités qu'il
importait de souligner, on généralise maintenant ces
notions.
4- les divers cas de figure à considérer :
Par convention, pour numéroter les effets, on place d'abord le symbole
du paradoxe qui est consolidé, puis on donne le numéro du premier
des 4 paradoxes qui interviennent dans sa consolidation.
Une fois désigné, grâce à son numéro, le
premier des paradoxes utilisés, les 3 autres s'en déduisent
aisément, puisqu'ils ne sont autres que les 3 paradoxes suivants dans
le tableau des 16 paradoxes. Étant précisé que le tableau
se lit comme une boucle continue : quand une ligne est terminée, on
passe au début de la suivante, et quand le tableau est terminé
on reprend à son début.
Lorsqu'un paradoxe est utilisé pour consolider l'un des 15 autres
paradoxes, son expression n'est pas la même s'il est en position initiale
(c'est-à-dire celui sur lequel le paradoxe à consolider s'appuie),
ou s'il est l'un des 3 paradoxes suivants.
Un tableau [aller à ce tableau] rend compte de ces deux cas de figure différents.
S'il vient en premier, il est complètement mobilisé pour lui-même
en tant que tel, c'est-à-dire que son expression est alors la véritable
expression spécifique de ce paradoxe, celle qui le différencie
le mieux de tous les autres paradoxes, celle où il est "le plus pur".
À l'occasion de la remise en cause complète que j'ai dû
faire pour élaborer cette nouvelle numérotation des paradoxes,
je me suis ainsi rendu compte que j'avais mal apprécié la nature
spécifique de deux des paradoxes : le "ça se suit / sans se
suivre", et le "même / différent". Dans le tableau évoqué
ci-dessus, j'ai indiqué en "nom secondaire", un nom qui correspond
mieux à leur spécificité, et qui d'ailleurs correspond
mieux aussi à la nature du phénomène physique qui m'a
servi à comprendre le fonctionnement de chacun.
Pour le "ça se suit / sans se suivre", ce phénomène
physique est le brassage brownien qui résorbe constamment, en les lissant,
les inégalités de vitesse ou de température qui existent
dans un gaz ou dans un corps [aller à l'explication plus détaillée].
L'expression "équilibré / dissymétrique" ou bien
encore l'expression "à égalité / classés"
(à
même vitesse selon la moyenne statistique, à vitesses
différentes,
et donc classés selon leur vitesse, selon les vitesses locales et temporaires)
rendent mieux
compte de ce fonctionnement.
Pour le "même / différent", il s'agit de la mise ensemble de
plusieurs tourbillons semblables pour construire un plus gros tourbillon
qui les combine sans les mélanger [aller à l'explication plus
détaillée]. L'expression "du différent / dans du même" (différentes
fois la même chose pour construire une seule et même chose, par exemple, différentes fois le même
tourbillon pour faire un seul plus gros tourbillon) rend mieux compte de ce fonctionnement.
Je conserve toutefois comme "nom principal" le nom initial
de ces deux paradoxes. À l'usage, et avec un peu plus de recul, je
verrai s'il convient de modifier le nom de ces deux paradoxes.
Si le paradoxe ne vient pas en premier, mais s'il est en deuxième
position, ou en troisième, ou en position de clef pour résumer
l'appui, alors il perd sa "pureté", et il prend au contraire une expression
qui l'apparente au paradoxe qui le suit.
Je suppose que cela provient du fait que, puisque chaque paradoxe est intrinsèquement
déjà contenu dans les paradoxes qui le voisinent [aller à
un exemple de ce principe], il est dopé par sa présence
partielle déjà là dans le paradoxe qui vient en premier,
ce qui le propulse alors à presque valoir le paradoxe qui le suit.
Je rappelle que, d'un certain point de vue, chaque paradoxe successif correspond
à un cran de plus de la complexité [aller à l'explication
plus détaillée]. Par conséquent, renforcer un paradoxe
l'amène à le faire muter dans le paradoxe suivant.
C'est cet aspect "dopé" que j'avais initialement pris pour l'aspect
"pur" des deux paradoxes mal nommés que j'ai évoqués
plus haut, le "ça se suit / sans se suivre", et le "même / différent".
Lorsque le paradoxe à considérer est celui-là même
qui est consolidé par 4 autres, deux cas de figure sont également
à distinguer qui sont détaillés dans un autre tableau
[aller à ce tableau].
En effet, si le paradoxe sur lequel il s'appuie fait partie des 3 paradoxes
qui le précèdent, il va donc se trouver lui-même à
former l'un des 3 paradoxes qui complètent cet appui, soit en deuxième
position, soit en troisième, soit même en position de clef pour
résumer lui-même l'appui que lui font les 3 autres.
Dans ces 3 circonstances, la particularité du paradoxe est que ses
deux aspects contradictoires ne vont pas se combattre directement mais qu'ils
seront, au contraire, physiquement séparés sur la forme. Peut-être
cela tient-il à la situation de faiblesse qui fait que, dans un tel
cas, il ne peut en fait compter que sur 2 autres paradoxes pour le consolider
au lieu de 3, ce qui l'obligerait à compenser en ne confrontant pas
ses deux aspects contraires de façon trop virulente.
Ou peut-être, cela tient-il à une "clarification d'expression"
qui lui serait utile, dans un tel cas, pour bien se différencier des
paradoxes qu'il utilise pour se consolider.
Dans le cas courant, c'est-à-dire lorsque le paradoxe est consolidé
en premier par l'un quelconque des 12 paradoxes qui le suivent, alors son
expression est plus directement conflictuelle, ses deux aspects contraires
portant leur conflit à l'intérieur d'une même forme.
Je dois attirer l'attention sur le fait que ces 2 cas de figure valent indifféremment
pour les expressions analytiques et les expressions synthétiques,
ce qui ne simplifie pas la différenciation de ces deux effets. Afin
de clarifier au mieux ce point, je me suis astreint, dans la présentation
de chacun des 480 effets à considérer (16 x 15 x 2 = 480),
à justifier pour quelle raison je le classais comme analytique ou
comme synthétique.
5- un peu de recul :
On a expliqué plus haut [y retourner] que l'appui qu'un paradoxe prend
sur un autre procède par 4 stades de complexité successifs.
Pour voir les choses de plus haut, on peut remarquer que le principe même
de l'appui d'un paradoxe sur un autre relève, lui aussi, de l'un
de ces 4 stades. Résumons en effet la façon dont on procède
:
0- racine fondamentale : on constate d'abord qu'il y a
du paradoxe, c'est-à-dire des faits paradoxaux. Cela constitue la
phase d'émergence ponctuelle des paradoxes, phase qui est le préalable
à leur mise en relation
1- on constate ensuite que tous les paradoxes ne se valent
pas entre eux, mais qu'on peut les différencier les uns des autres
selon leurs propriétés particulières. C'est la phase
du classement des paradoxes entre eux
2- on croise ensuite les propriétés de deux
paradoxes, l'un servant de base, et l'autre d'appui transverse servant à
soutenir le premier. C'est la phase de l'organisation, celle précisément
qui construit l'appui d'un paradoxe sur un autre, appui qui est l'objet du
présent texte
3- enfin, le tout se noue lorsque l'artiste fixe ces relations
dans un jeu de formes qui permet de les conserver sous l'aspect d'une oeuvre
d'art. C'est la phase de la clef, celle qui permet à l'artiste de
fixer, d'oeuvre en oeuvre, ce qu'il réussit péniblement à
faire émerger comme relations significatives, pour lui, entre les
diverses formes.
Il est rappelé que l'artiste qui invente ainsi le jeu de forme qui lui est utile
pour rendre tangible et pour conserver les effets paradoxaux indicibles qu'il
sent sourdre en lui, ne doit pas seulement isoler de telles combinaisons duales
de paradoxes. Il doit aussi, ainsi qu'on le montre dans d'autres textes [aller
à l'un de ces textes], combiner quatre telles combinaisons, chacune
appelée "paradoxe d'état", plus deux à quatre combinaisons,
chacune appelée "paradoxe de transformation".
6- mises à jour futures :
La totalité des 480 effets possibles est dès à
présent réunie dans le "catalogue" en ligne.
Je me suis efforcé d'expliciter pour chacun les raisons pour lesquelles
la numérotation me semblait appropriée, en expliquant le rôle,
dans cet effet, de chacun des 4 paradoxes qui viennent en appui d'un autre.
La règle utilisée est celle qui est résumée dans
les deux tableaux présentés plus haut, et, en principe, n'importe
qui peut donc chercher à utiliser cette règle, vérifier
si mon classement est pertinent. N'hésitez pas à me signaler
une erreur qui vous apparaîtrait.
À l'usage, c'est-à-dire avec l'expérience de l'habitude,
je m'attends à devoir de temps en temps modifier quelques classements,
même si personne ne me signale d'erreur, simplement parce que je vais
chercher à classer un jeu de forme que je n'avais pas encore envisagé
et dont je devrai bien constater qu'il correspond mieux à l'un des
numéros d'effets que celui actuellement placé sous ce numéro.
Je tiendrai à jour une page spéciale [y aller] dans laquelle
je ferai l'historique de ces corrections . . . que j'espère les
moins nombreuses possible.
Toutefois, il faut bien comprendre que tous les effets plastiques possibles
ne sont pas dès à présent réunis, ou plus exactement
il faut dire : tous les moyens plastiques utilisables pour
obtenir tous les 480 effets paradoxaux possibles ne sont pas réunis.
Selon que l'artiste utilise des lignes, ou des couleurs, ou des volumes,
ou des espaces construits, ou des combinaisons de ces différents moyens,
il est amené à s'y prendre différemment pour obtenir
l'effet paradoxal recherché.
On peut aller par exemple à l'effet a2 où 3 moyens
ont été répertoriés qui permettent d'obtenir le même
effet, chacun correspondant à un nombre différent de dimensions de la figure utilisée.
où 3 moyens
ont été répertoriés qui permettent d'obtenir le même
effet, chacun correspondant à un nombre différent de dimensions de la figure utilisée.
Au fur et à mesure de mes trouvailles, je compléterai ma bibliothèque,
mais ces additions-là ne seront pas répertoriées sur
la page présentant l'historique des rectifications de mes erreurs.
le 1er janvier 2005

 du paradoxe "continu / coupé", expression qui s'appuie
précisément sur le paradoxe "un / multiple", les colonnes
de la Grèce Hellenistique données en référence, ou bien la
femme/bâton de de Dolni Vestonice à l'époque
préhistorique, proposent également des exemples
semblables de lignes continues / coupés, en tablant sur le
changement de texture (lisse / cannelé ou lisse / rayé)
au lieu du changement de couleur.
du paradoxe "continu / coupé", expression qui s'appuie
précisément sur le paradoxe "un / multiple", les colonnes
de la Grèce Hellenistique données en référence, ou bien la
femme/bâton de de Dolni Vestonice à l'époque
préhistorique, proposent également des exemples
semblables de lignes continues / coupés, en tablant sur le
changement de texture (lisse / cannelé ou lisse / rayé)
au lieu du changement de couleur. du "continu / coupé", où le paradoxe "rassembler /
séparer" lui sert d'appui, où le "continu / coupé"
est à la place du paradoxe qui organise son propre appui, et
où le "lié / indépendant" sert à nouer cet
appui. Parmi les exemples que vous trouverez en suivant le lien
ci-dessus correspondant à cette expression, celui de
référence (le cercle des Sarsens de Stonehenge) et les
"Cambell's Soup Can" de Warhol correspondent à l'usage d'une
ligne continue / coupée comme on l'a évoqué avec
le petit schéma ci-dessus.
du "continu / coupé", où le paradoxe "rassembler /
séparer" lui sert d'appui, où le "continu / coupé"
est à la place du paradoxe qui organise son propre appui, et
où le "lié / indépendant" sert à nouer cet
appui. Parmi les exemples que vous trouverez en suivant le lien
ci-dessus correspondant à cette expression, celui de
référence (le cercle des Sarsens de Stonehenge) et les
"Cambell's Soup Can" de Warhol correspondent à l'usage d'une
ligne continue / coupée comme on l'a évoqué avec
le petit schéma ci-dessus.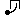 où 3 moyens
ont été répertoriés qui permettent d'obtenir le même
effet, chacun correspondant à un nombre différent de dimensions de la figure utilisée.
où 3 moyens
ont été répertoriés qui permettent d'obtenir le même
effet, chacun correspondant à un nombre différent de dimensions de la figure utilisée.