I 
accueil		 E 
sommaire Mathématique		 suite :    F 
mesure de la déformation d'un contraste
accès direct à tous les autres textes de la section ----> 00 01 02 03 10 11 12 20  21 30 31 32 33 34
 
RAPPEL : une version de l'ensemble du développement, revue et améliorée dans le détail, est disponible en format pdf à l'adresse : Dimensions des nombres  

 
 
 
Qu'est-ce qu'une dimension ?
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
  
             L'idée essentielle développée dans les textes qui suivent est que les nombres ne sont pas toujours à une seule dimension, mais qu'un nombre tel que "2" peut aussi bien être la mesure d'une dimension de longueur, que la mesure d'une surface ou d'un volume.  
             Cela ne signifie pas seulement que l'on peut mettre une unité "m", "m2" ou "m3" derrière lui, mais surtout qu'il ne va pas se calculer de la même façon selon le nombre des dimensions qu'il porte : 2 x 2 x 2 ne donnera pas le même résultat selon que les "2" en question ont 1, 2, 3 ou 4 dimensions.  
 
 
Avant de développer cette idée, nous faisons un historique rapide de la notion de dimension.
 
 

De la longueur des choses jusqu'aux degrés de libertés

Dans l'antiquité, lorsqu'on parlait d'une dimension, on pensait soit à la hauteur, soit à la longueur, soit à la largeur d'une chose. 
 
 
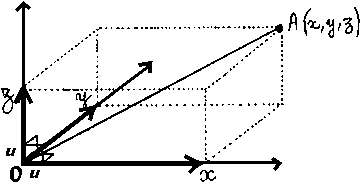Au XVIIème siècle, Descartes en donna une définition plus générale. Pour lui, une dimension est une coordonnée que l'on mesure dans un repère d'axes. Dans cette façon de voir, la hauteur, la longueur et la largeur ne correspondent plus qu'à un cas particulier de coordonnée, celui où les trois axes sont orthogonaux entre eux et sont mesurés avec une même unité de longueur. Usuellement, on dit que ce sont les coordonnées de l'espace euclidien. 
Cette définition se montra spécialement utile pour décrire le mouvement d'un point dans l'espace, et a été exploitée au mieux par la mécanique de Newton, par exemple pour décrire le mouvement de la terre dans son orbite autour du soleil. 
 
 
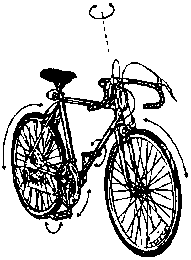
Au milieu du XIXème siècle, le mathématicien Riemann donna une interprétation encore plus générale de la notion de dimension. Puisqu'un phénomène évolue sous l'influence de divers paramètres, Riemann suggéra que l'on attribue une coordonnée distincte à chacun de ces paramètres. De nos jours on appelle ces paramètres des "degrés de liberté". L'importante nouveauté de cette conception est que rien ne nous empêche de donner à chaque point plus que trois coordonnées.
On cite ici l'exemple que Ian Stewart donne des dimensions du mouvement d'une bicyclette dans son livre "Dieu Joue-t-il aux dés ?"  :
'Une bicyclette a (selon une estimation réductrice) cinq parties mobiles principales : le guidon, la roue avant, l'assemblage essieu-chaîne-roue arrière, et deux pédales. Chacune de ces parties nécessite pour être décrite une coordonnée de position et une coordonnée de vitesse : un ingénieur dirait qu'elle a "dix degrés de liberté". Pour faire de la bicyclette, vous devez sentir le mouvement d'un point dans un espace à 10 dimensions ! C'est peut-être pour cela que c'est si difficile à apprendre.'   
[Ian Stewart - Dieu Joue-t-il aux dés ? - Flammarion 1992]
 
 
  
Ainsi donc, une dimension fut tout d'abord considérée comme un aspect très concret des objets.  
Puis la dimension devint la coordonnée d'un point se déplaçant dans un espace réel à trois dimensions.  
Puis une coordonnée devint un degré de liberté dans un espace à "n" dimensions, "n" pouvant être aussi grand que l'on veut. 
 
 

 
 

Chaos déterministe et dimensions fractales

Ces dernières années, cette définition des dimensions comme "coordonnées d'un point" ne fut pas remise en question, mais elle commence à poser un problème.
Elle pose un problème depuis que Benoit Mandelbrot a montré la pertinence qu'il y a bien souvent à utiliser des dimensions d'espace fractionnaires. Une dimension fractionnaire (on dit "fractale"), c'est par exemple une dimension 1,3897. Parler d'un point dans un espace à 6 ou 10 dimensions, on peut le concevoir comme une simple extension de ce que l'on conçoit dans un espace à 3 dimensions : c'est plus compliqué, mais c'est toujours un peu la même chose. Mais les coordonnées d'un point dans un espace à 1,3897 dimensions, qu'est-ce que cela peut bien signifier? À quoi cela peut-il ressembler ? Cela ne peut plus être seulement "un peu plus compliqué" qu'un espace de dimension 1 ou 2, on sent bien que cela doit être "autre chose" de tout différent. Pour le moins, c'est bizarre.

Par ailleurs, il a bien fallu que les scientifiques finissent par reconnaître qu'ils laissaient de côté de nombreux phénomènes naturels fréquents mais qu'ils ne parvenaient pas à calculer. Par exemple, quelque chose d'aussi simple et banal que celui-ci : lancez un bouchon dans un fleuve, et demandez-vous où il sera dans une heure : toujours à la même place, prisonnier d'un tourbillon? Ou très en aval ? Ou très en amont, et peut-être sur l'autre rive, emporté par une série de contre-courants ? Aucune équation ne peut vous aider à prévoir la réponse.
Des équations peuvent vous permettre de calculer avec une précision diabolique l'évolution des coordonnées d'une sonde lancée dans l'espace entre les planètes. Mais elles vous laisseront désemparés si vous voulez prédire avec la moindre précision l'évolution des coordonnées d'une feuille qui tombe d'un arbre, juste devant votre nez, ballotée dans un très léger courant d'air.

Dans le jargon scientifique d'aujourd'hui, on appelle ces phénomènes insolubles en équations, le "chaos déterministe". Déterministe, parce que des effets objectifs et précisément mesurables et repérables déterminent la suite des évènements. Chaos, parce qu'on ne sait pas du tout ce qui va se passer, malgré la connaissance que nous avons de toutes les données qui déterminent les évènements.
Et du chaos déterministe, on finit par s'apercevoir que cela fourmille dans la nature. Les mouvements de l'eau ou de l'air par exemple, sont dans bien des situations chaotiques. Mais pour avoir le chaos déterministe, vous avez juste besoin de prendre 3 corps et de chercher leur influence réciproque. La terre qui tourne autour du soleil, c'est parfaitement décrit par une équation. Mais la terre, plus la lune, plus le soleil, et leurs attractions réciproques, c'est déjà fondamentalement imprévisible. On y arrive en bricolant les équations par des approximations et des corrections pas très limpides d'un point de vue mathématique, mais on y arrive parce que les planètes ne tournent pas vite, et que l'on ne cherche pas à savoir ce qui se passera dans des milliards d'années. À la question : "le système solaire est-il stable ?", personne n'a encore apporté de réponse certaine.

L'explication usuelle est de dire que l'imprévisibilité de tels phénomènes résulte d'une "sensibilité extrême aux conditions initiales". Vous lancez le bouchon dans le fleuve une fraction de millimètre plus à gauche ou à droite, et son voyage dans le fleuve en sera tout différent simplement parce qu'un très petit écart au départ se trouvera amplifié au cours de son trajet. Cet écart sera de plus en plus amplifié au fur et à mesure que le temps passe, et finalement cela le dirigera vers un tourbillon faisant du sur-place, ou vers un courant régulier bien installé qui le mènera rapidement vers l'aval. Or pour calculer un mouvement, il faut bien arrondir les résultats d'un calcul avant de passer au suivant, puisque cela ne tombe jamais "juste". Quelle que soit la précision que l'on s'accorde, il reste un infime écart d'arrondi dans le résultat. Cet infime écart s'amplifie lui aussi au cours des calculs successifs, et il finit par être suffisamment important pour fausser complètement le résultat de l'évolution que l'on cherchait à prévoir.
 
 

Pour une nouvelle définition des dimensions

 
  
Nous allons essayer de proposer un nouvel angle d'attaque de ce type de problème, et suggérer que l'impuissance à décrire par une équation l'évolution des coordonnées d'un point dans un phénomène chaotique, ne proviendrait pas d'une réelle imprévisibilité du phénomène. Elle résulterait plus simplement de l'inadaptation de notre manière de représenter ces phénomènes, c'est-à-dire de les dimensionner.  
Le problème ne serait pas sans solution, il serait seulement mal posé.  
Et nous ne le posons pas correctement, précisément parce que nous le posons en terme de coordonnées de dimensions, c'est-à-dire en terme de trajets de points dont les coordonnées évoluent dans l'espace et dans le temps.  
  
Nous essaierons de démontrer qu'une définition entièrement nouvelle des dimensions est requise, plus générale encore que celle de coordonnées dans un espace à "n" dimensions.  
 
Dans cette définition, une coordonnée ne sera plus à son tour qu'une espèce spéciale de dimensions, et considérer la trajectoire de points sera seulement une manière parmi d'autres de décrire l'évolution d'un processus. Une manière parfois utile, mais parfois complètement inappropriée.
Avec cette définition, les dimensions fractionnaires de Mandelbrot perdront leur aspect bizarre, et apparaîtront même plus naturelles et plus normales que les dimensions entières que l'on utilise pour décrire l'espace euclidien.
 

La conception actuelle définit une dimension comme la valeur que l'on donne à une coordonnée.
Pour résumer la définition nouvelle que l'on va proposer ici, on dira qu'une dimension est la valeur que l'on donne à une déformation.
De façon générale, nous parlerons d'ailleurs de "dimensions de déformation".
Qu'est-ce donc qu'une dimension de déformation ?
Pour d'abord introduire le lien essentiel entre dimension et déformation, nous commencerons par montrer qu'on peut très bien mesurer certaines déformations sans jamais utiliser la moindre coordonnée.
 

I 

 accueil 

 E 

Math

 G 

 haut 

 suite :    F   mesure de la déformation d'un contraste
O
 
auteur