Nous avons vu comment des dimensions courbes permettent de décrire l'évolution d'un contraste. Nous allons voir maintenant comment elles permettent aussi de mesurer des trajets. Le point important à comprendre à ce propos, est qu'il ne faut pas confondre la "courbe" que décrit un mobile, c'est-à-dire son trajet, et les valeurs "courbes" de la déformation qui fait bouger le mobile, et qui provoque donc ce trajet.
En effet, ce que l'on va chercher à décrire, ce n'est pas la forme du parcours lui-même qui ne sera qu'une résultante de la dimension de déformation, mais c'est l'organisation des forces qui s'appliquent en un point, et qui précisément le forcent à se déplacer.
 
 

Fondamentalement, c'est à décrire l'effet d'un champ de force, par exemple un champ électromagnétique, que sera utile cette dimension.  Habituellement, un tel champ est représenté par un ensemble de vecteurs qui, en tous points, décrivent la direction et la vitesse d'un écoulement. Ce qu'on sait bien exprimer en terme de coordonnées (exemple ci-contre).   [image tirée d'un article de G. Hooft : les théories de jauge et les particules élémentaires - Pour la Science]

 
 

L'originalité de la démarche que nous proposons, consiste à ne pas cumuler en chaque point de l'espace l'ensemble des sollicitations qui s'exercent sur lui, à ne pas les résumer en un seul vecteur. Nous proposons au contraire de laisser ouvert, "non résolu", le cumul de ces sollicitations.  Dans le cas général il reste donc en chaque point du champ de force une infinité de vecteurs. Chacun indique dans une direction spécifique, l'intensité de la sollicitation qui s'exerce en ce point et selon cette direction.

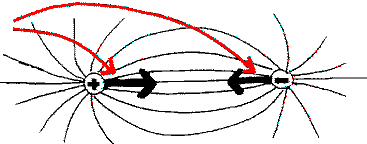
Par exemple, dans le cas de deux charges électriques de signes contraires, le champ de forces se représente par une série de courbes reliant les deux charges. Dans un système de coordonnées, l'effet de ce champ est résumé par 2 vecteurs dirigés depuis chaque charge vers l'autre : elles s'attirent d'un centre à l'autre, et ces 2 vecteurs décrivent l'intensité et la direction de cette attraction.
 

usuellement, l'attraction entre les 2 charges électriques est résumée par 2 vecteurs

 
 
Dans notre système de représentation, nous n'allons plus "résumer" l'effet des champs électriques, mais au contraire le maintenir étalé dans toutes les directions de l'espace. Chaque ligne de champ correspond à un effet spécifique, à une sollicitation particulière vers l'autre charge. Nous représentons pour chaque ligne la direction de cette sollicitation : tangente à la courbe, et son intensité : plus elle pointe vers le centre de l'autre charge, plus elle est grande.
En passant, on note que si les 2 charges sont faibles, ou si toutes 2 sont fortes, les dessins auront la même allure, et se déduiront simplement l'un de l'autre par homothétie. Bref, ils seront auto-similaires.
 

notre proposition  pour représenter  la même attraction  électrique

 

L'allure de ce graphique ressemble à un coeur. Il est truffé de vecteurs dont l'intensité varie entre un minimum et un maximum. C'est là le premier aspect "courbe" de la grandeur, puisqu'elle tourne en rond sur un cercle allant de 0/1 à 1/0.
Si l'on calculait la résultante de tous ces vecteurs, elle serait un vecteur unique, qui dirait la direction et la vitesse de la courbe que décrit la charge en se déplaçant. C'est là le deuxième aspect "courbe" de cette dimension, celui que nous allons négliger.
 

Au premier abord, cela peut sembler compliquer les choses que de s'abstenir de réduire l'ensemble des sollicitations en un point à un vecteur unique.
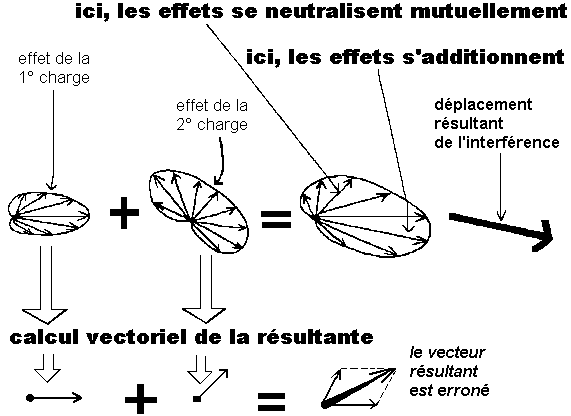
Envisageons cependant le cas d'une charge qui n'est pas soumise qu'à une seule autre charge, mais qui est soumise à deux charges distinctes.
Chaque charge donne alors lieu à une dimension de déformation courbe qui sont toutes les deux centrées sur le même point. Entre ces deux dimensions, peuvent se créer des effets d'accord ou d'opposition entre leurs formes respectives. Ces effets peuvent se cumuler dans certaines directions, et s'annuler dans d'autres directions. Un simple vecteur ne pourra pas garder trace de tels accords ou désaccords de phases, et seul un étalement complet des sollicitations dans toutes les directions permet de ne pas gommer la complexité des interférences dont l'intensité varie selon les directions de l'espace. Or précisément, la compréhension de l'évolution d'un phénomène réside souvent dans l'allure des interférences entre les paramètres multiples qui le régissent.