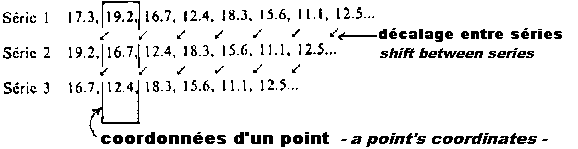
| I
accueil |
E
sommaire Mathématique |
avant
: E
la continuité des déformations dans l'espace |
suite
: F
naissance d'une dimension |
| accès direct à tous les autres textes de la section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
|
On ouvre très doucement un robinet. Une goutte se forme petit à petit, se gonfle, puis se détache et fait "floc" en tombant sur l'évier. Si l'on écoute tomber les gouttes les unes après les autres, on entend alors "floc-floc-floc, etc.". On ouvre encore un tout petit peu plus le robinet, et les gouttes commencent à se grouper par deux : deux gouttes très rapprochées, puis un intervalle un peu plus long, et à nouveau deux gouttes très rapprochées. On entend maintenant : "flicfloc-flicfloc-flicfloc, etc". On ouvre encore d'avantage le robinet, le rythme des flicflocs s'accélère. Plus on ouvre, plus l'intervalle entre un flic et un floc se réduit, et plus l'intervalle entre un flicfloc et un autre flicfloc se réduit également. On ouvre encore un peu plus, juste une fraction de soupçon de presque rien d'un peu plus, et alors soudain, sans raison apparente, le rythme des gouttes devient complètement irrégulier, sans plus aucune périodicité, en un mot : complètement chaotique. |
La chose
a été mesurée expérimentalement.
Ian Stewart le signale dans son même ouvrage mais cette fois au chapitre "Retour à Bashô".
Robert Shaw et ses collaborateurs
à l'université de Californie à Santa Cruz, ont commencé
par réaliser une mesure sur environ 5 000 intervalles successifs
de temps entre gouttes dans la phase "chaotique" d'un robinet. Le rythme
obtenu avait bien un aspect absolument aléatoire dont aucune régularité
ne pouvait être décelée.
Puis, cette équipe a procédé
à ce que Ian Stewart appelle un "trucage", et qui a consisté
à construire une figure 3 D à l'aide de la série purement
linéaire (donc apparemment 1 D) des intervalles de temps mesurés.
Le trucage est le suivant : on utilise
la valeur d'un intervalle de temps comme 1ère coordonnée
d'un point dans l'espace. Pour obtenir la 2ème coordonnée
du même point on prend la valeur de l'intervalle mesuré juste
après. Et pour obtenir la 3ème coordonnée on prend
la valeur de l'intervalle mesuré encore après. Puis la valeur
qui a servi de 2ème coordonnée est maintenant prise comme
1ère coordonnée d'un nouveau point, etc. Ce trucage, transformant
une série 1 D en figure 3 D, est une méthode mise au point par Ruelle, Packard et Takens.
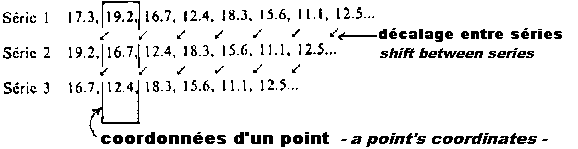
 Etrangement,
dans le cas des intervalles chaotiques entre gouttes, tous
les points obtenus par ce type de bricolage d'une série apparemment
aléatoire et irrégulière construisent dans l'espace
une figure bien formée. Etrangement,
dans le cas des intervalles chaotiques entre gouttes, tous
les points obtenus par ce type de bricolage d'une série apparemment
aléatoire et irrégulière construisent dans l'espace
une figure bien formée.
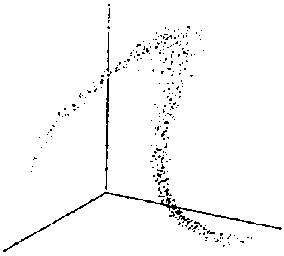
Ils se tiennent tous à l'intérieur de la surface de la figure que l'on reproduit ci-contre. |
Etrangement est le mot, puisque l'on
donne précisément à cette figure le nom "d'attracteur
étrange".
Attracteur,
car tous les points y sont attirés.
Etrange,
car ils ne forment pas une figure continue dans le temps. Si par exemple
un point calculé tombe vers un bout de la figure, on ne peut absolument
pas deviner si le suivant de la série sera juste à côté,
ou à l'autre bout de la figure. Il sera tout simplement n'importe
où, mais toujours à l'intérieur de la surface que
forme la figure.
|
Nous étions partis d'une série temporelle 1 D continue, puisque les intervalles de temps y sont rangés dans l'ordre exact où ils se sont produit l'un après l'autre, en continu dans le temps. La figure que l'on a formée a gagné plusieurs dimensions, mais "en échange" elle a perdu toute continuité dans la dimension du temps. Que s'est-il donc passé ? Pour le deviner, nous allons maintenant réinterpréter la dynamique des gouttes en termes de déformations. |
Et
puis soudain, n'importe quoi : le chaos.
Les trois déformations que
l'on a décrites sont ce qu'on a appelé des "déformations
courbes" [revoir E
ce moment],
car leurs valeurs varient de façon périodique :
-
ainsi, la pression de l'eau qui force la goutte à se gonfler
passe par un maximum que l'on peut quantifier comme "1" et qui équivaut
à un redémarrage à 0, puisque la goutte libérée
quitte alors le robinet.
-
même chose enfin pour la gravité qui s'exerce sur le
volume d'une goutte d'eau qui augmente jusqu'à un maximum puis repart
à 0 quand la goutte est tombée.
-
même chose pour la tension capillaire qui varie périodiquement
avec la forme périodiquement plus ou moins tendue de la goutte.
Par ailleurs, ces
trois déformations courbes sont incommensurables entre elles :
il n'y a pas de relation stricte entre ce qui modifie la pression de l'eau
(notre main qui tourne le robinet), ce qui fait varier l'intensité
de la capillarité (la forme de la goutte qui change continuellement),
et ce qui fait varier le volume d'eau pris en charge de façon cohérente
et continue par la gravité (la viscosité interne du liquide).
Malgré
cette incommensurabilité, l'effet cumulé de ces trois causes
de déformation est d'abord "continu" dans l'espace-temps :
on voit bien chaque goutte naître, se gonfler, tomber.
C'est sans surprise.
Quand on augmente la pression, on
force les trois causes à interférer les unes avec les autres
car on ne laisse pas le temps à une goutte de tomber avant de provoquer
la naissance d'une autre. Mais bien que ce soit déjà un peu
compliqué, c'est toujours continu, c'est-à-dire que l'on
peut toujours deviner ce qui va se passer, comment le rythme va accélérer.
Puis,
quand l'interférence atteint un point particulier, soudainement
cela n'est plus du tout continu dans l'espace-temps,
parce qu'on ne pourra plus jamais déduire de ce qui s'est passé
dans l'espace à un instant, ce qui se passera dans l'espace à
l'instant suivant : le prochain intervalle entre gouttes sera-t-il plus
court que le précédent ? sera-t-il plus long ? sera-t-il
semblable ?
Nous ne pouvons plus répondre,
car il
n'y a plus aucune continuité
repérable dans le rythme.
| I
accueil |
E
Math |
G
haut |
suite : F naissance d'une dimension |
|