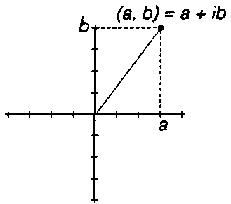I
accueil |
E
sommaire
Mathématique |
|
avant
: E
pour voir se qui se passe dans la 4ème dimension |
RAPPEL : une version de l'ensemble du développement, revue et améliorée dans le détail, est disponible en format pdf à l'adresse : Dimensions des nombres
Dimensions en chaîne
Quand une courbe se dessine au cours du temps, ses points passent d'une position à l'autre de cette courbe.
Avec un attracteur étrange, on ne voit plus des points parcourir une courbe, mais sauter d'un endroit à l'autre d'une surface ?
Eh bien, il faut se rendre à l'évidence : un attracteur étrange
ne représente pas l'évolution d'une courbe, mais celle d'une surface.
Nous allons faire l'hypothèse
que cette mutation de la figure par augmentation du nombre de ses dimensions
(surface 2D remplaçant une courbe 1D) aurait à voir avec
la mutation de la dimension fractale représentée : une courbe
représenterait une dimension fractale "1" et une surface représenterait
une dimension fractale "2".
Mais on ne peut comprendre la signification
de cette mutation si l'on ne considère que le fonctionnement d'un
attracteur étrange, aussi nous devons maintenant proposer une hypothèse
générale sur l'enchaînement
de tous les types de dimensions. Pour présenter notre hypothèse,
nous la résumons dans un tableau.
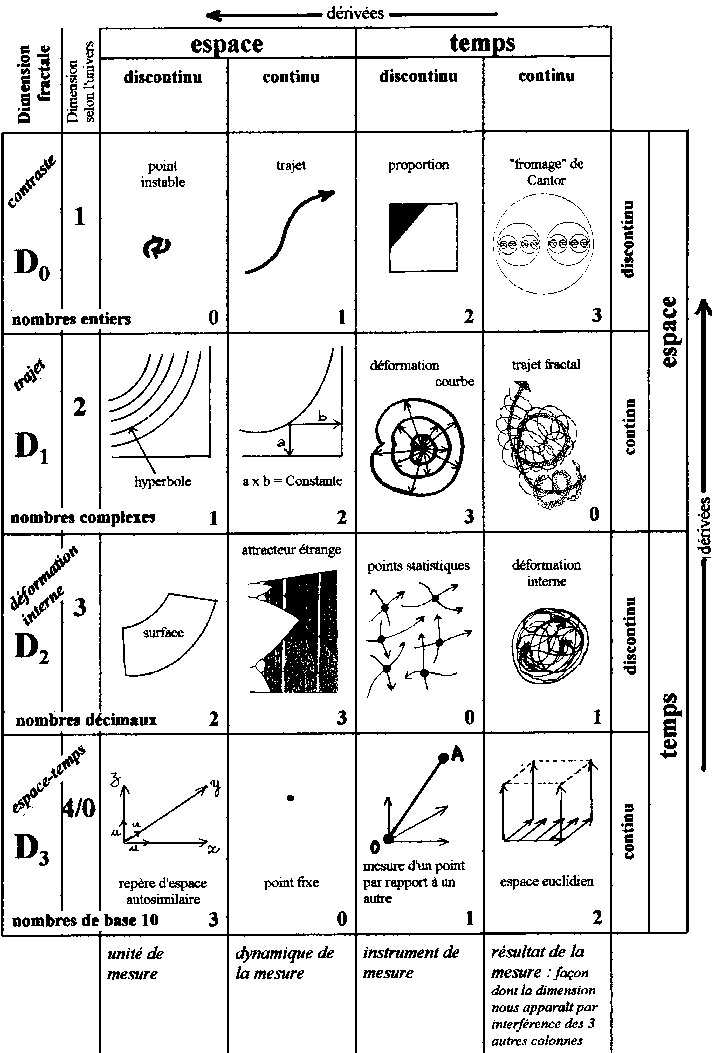
Chaque ligne horizontale correspond
à une dimension fractale, comptée de 0 à 3.
-
dans la 1ère
ligne, se trouve la dimension fractale qui a pour partie entière
0, et dont nous
avons dit qu'elle était spécialement adaptée pour
mesurer des contrastes [revoir
E cela].
Les 2 premières cases de
cette ligne montrent un fonctionnement analogue à celui que l'on
a décrit pour le mode de génération des nombres entiers
: instabilité du 0 dont la vibration dévide d'un coup tous
les nombres jusqu'à l'infini [revoir
E
le chapitre "Reprenons
à partir de zéro"].
Nous dirons donc que cette dimension
fractale 0 est celle des nombres entiers.
-
dans la 2ème
ligne, se trouve la dimension fractale qui a pour partie entière
1, et dont nous
avons dit qu'elle était spécialement adaptée pour
mesurer des trajets [revoir
E cela].
Cette dimension fonctionne par la
mesure simultanée de deux grandeurs, comme cette caractéristique
est aussi celle des nombres complexes, nous dirons donc que cette dimension
fractale 1 est celle des nombres complexes.
|
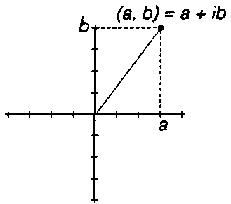 |
les
nombres complexes peuvent s'écrire
a + ib
(ou i est la racine carrée de -1)
ou être
représentées par un couple de nombre (a,b) |
-
dans la 3ème
ligne, se trouve la dimension fractale qui a pour partie entière
2, et dont nous
avons dit qu'elle était spécialement adaptée pour
mesurer la déformation interne des corps [revoir
E cela].
Dans le chapitre "Reprenons
à partir de zéro" [revoir
E ce
chapitre],
nous avons expliqué pourquoi les nombres décimaux réclament
une dimension 2 pour être produits et conservés, nous dirons
donc que cette dimension fractale 2 est celle des nombres décimaux.
-
dans la 4ème
ligne, se trouve la dimension fractale qui a pour partie entière
3. Jusqu'ici nous
n'avons pas encore proposé de signification à ce type de
dimension.
Nous suggérons maintenant
que cette dimension soit celle de l'espace-temps et des repères
d'espace-temps tels qu'on les considère habituellement.
La dimension 3 étant spécialisée
dans l'interférence des dimensions qui la précédent,
nous proposons de considérer cette dimension comme étant
celle qui permet de combiner la dimension des nombres entiers, celle des
nombres complexes et celle des nombres décimaux.
Comme c'est l'introduction des nombres
de base 10 qui permet de calculer de façon commode les nombres dans
tous les cas de figure, nous dirons donc que la dimension 3 est la dimension
des nombres de base 10.
La 1ère ligne correspond donc
aux dimensions fractales qui ont 0 pour partie entière. Comme nous l'avons déjà suggéré, ces dimensions servent à calculer les contrastes.
|
- dans la
1ère colonne, nous trouvons la figure mathématique qui
permet de réaliser la mesure [la légende
décrivant la fonction de chaque colonne est en bas du tableau].
Comme un contraste peut se mesurer par un rapport entre deux grandeurs,
le résultat de ce rapport est simplement un nombre, et un nombre
peut toujours être représenté à l'aide d'un
point sur un axe. La 1ère case est donc ici illustrée par
un point, mais comme ce point n'est pas fixe et qu'il est au contraire
susceptible de se déplacer sans cesse sur une courbe, on dira qu'il
s'agit d'un point "non stabilisé". C'est le déséquilibre
perpétuel d'un tel point sous l'effet de sa contradiction interne,
qui provoquerait son déplacement incessant.
- dans
la 2ème colonne, on trouve la dynamique avec laquelle fonctionne
l'instrument de mesure décrit en 1ère case. Comme on vient
de le dire, la dynamique d'un point instable, c'est une courbe. On peut
dire aussi un trajet.
- la
3ème colonne correspond à la façon dont s'opère
la mesure de la dimension. Ce que l'on mesure en fait, c'est l'effet provoqué
par la déformation sur le milieu où elle s'exerce. La nature
de la mesure dépend de la nature de cette réaction du milieu.
Ici, la déformation consiste à provoquer un contraste, c'est
donc sous la forme d'une mesure de proportion que se fait sa mesure.
- dans
la 4ème colonne, nous trouvons la façon dont s'organise
la déformation mesurée, c'est-à-dire finalement la
façon dont le phénomène nous apparaît dans la
réalité. Ici, nous avons donné l'exemple du "fromage"
de Cantor qui se construit comme une poussière de Cantor [revoir
E une
poussière de Cantor]
à partir d'une proportion que l'on retrouve identique à toutes
les échelles de lecture.
Dans chaque coin de case, nous avons
une valeur de dimension qui permet de lire le tableau dans un ordre de
progression diagonal. C'est une lecture qui est donc à la fois croisée
avec la progression des lignes et avec la progression des colonnes.
On remarque que sur chaque diagonale
lue du bas à gauche vers le haut à droite, les dimensions
sont les mêmes. Cela signifie que la progression diagonale est équilibrée
pour toutes les cases dans le sens de lecture des diagonales qui vont du
haut à gauche vers le bas à droite.
Quand on tombe sur la valeur
3, cela signifie que l'on est dans la case de la dimension où
s'exerce le caractère autosimilaire de la dimension fractale en
question.
Pour la dimension 0, c'est donc
en 4ème case qu'apparaît ce caractère, et la présence
du fromage de Cantor dans cette case est bien cohérente avec ce
caractère.
Quand on tombe sur la valeur
2, cela signifie que l'on est dans la case où s'exerce la valeur
décimale de la dimension.
Pour la dimension 0, c'est en 3ème
case qu'apparaît ce caractère, qui est donné par le résultat
de la proportion mesurée.
Quand on tombe sur la valeur
1, cela signifie que l'on est dans la case où s'exerce la fonction
complexe de la dimension.
Ici elle n'est pas très "complexe"
puisqu'il s'agit d'une seule courbe que l'on trouve en 2ème case.
Quand on tombe sur la valeur
0, cela signifie que l'on tombe sur la case qui exprime la valeur entière
de la dimension.
On la trouve ici en 1ère
case, qui est celle d'un point "même pas stabilisé". Le nombre
0 pour cette case semble approprié.
|
La 2ème ligne correspond aux dimensions fractales qui ont 1 pour partie
entière, et qui sont spécialement adaptées à calculer les trajets.
|
- dans sa
1ère case, nous avons mis l'état "de ce qui sert à
la mesurer" : ce sont des courbes hyperboliques. La caractéristique
d'une hyperbole est que pour tous ses points le produit de l'abscisse par
l'ordonnée a une valeur constante. Gauss, qui a donné aux
nombres complexes la présentation que les mathématiciens
utilisent toujours, a aussi montré que les nombres complexes avaient
à voir avec la courbure hyperbolique d'un espace. Ces travaux ont
trouvé leur plein accomplissement dans la notion de courbure de
l'espace par les masses qu'a proposée Einstein, ce calcul faisant
appel précisément aux nombres complexes. Nous rappelons que
selon la lecture diagonale et selon la lecture par lignes de notre tableau,
nous sommes avec cette case dans la dimension des nombres complexes.
- la
dynamique que l'on trouve en 2ème case a son origine dans ce
que l'on vient de dire sur la particularité d'une courbe hyperbolique
: ce qui a ici valeur de constante, ce n'est pas une seule valeur isolée
mais le produit de deux grandeurs, l'une qui sert d'abscisse et l'autre
qui sert d'ordonnée. La dynamique de cette dimension est donc celle
de la coordination continue de deux dimensions de type "0". Selon l'importance
respective de ces 2 dimensions variera la valeur décimale de la
dimension.
- en
3ème case, on trouve la façon dont s'organise sa synchronisation
à toutes les échelles (lecture diagonale) et la manière
dont la dimension s'exerce (lecture par colonnes). Elle s'exerce par une
impulsion de déplacement dans toutes les directions, que l'on a
représentée comme nous l'avons suggéré en début
de ce chapitre par une infinité de vecteurs pointant dans toutes
les directions possibles [revoir
E cette
représentation].
La forme spécifique de chaque "bouquet de vecteurs" est donnée
par la valeur décimale de la case précédente. La dimension
autosimilaire à toutes les échelles est donnée par
la forme identique à toutes les échelles de ce "bouquet".
- en
4ème case, on trouve la façon dont la dimension nous
apparaît sous l'effet de l'interférence de ses 3 premiers
aspects : elle nous apparaît comme un trajet. Dans l'espace, un trajet
correspond à une dimension entière "1". Selon la lecture diagonale du tableau, puisque l'on trouve la valeur 0 en coin de case, celle-ci doit indiquer la valeur de la partie entière de la dimension. Comme il s'agit de la ligne de la dimension fractale 1 et que l'on y trouve un trajet dont on a dit, au chapitre 9, qu'il correspondait à une dimension fractale qui a 1 pour partie entière, tout cela est cohérent.
Puisqu'il est question, ici, de trajet fractal, celui qui illustre cette case est similaire à lui-même sur toutes ses échelles : une hélice en hélice d'hélice.
La 3ème ligne correspond aux dimensions fractales qui ont 2 pour partie
entière, et qui sont spécialement adaptées à mesurer des déformations internes.
|
- dans sa
1ère case, nous avons mis l'état "de ce qui sert à
la mesurer" : ce sont des surfaces ainsi que nous l'avons vu dans notre
analyse des attracteurs étranges [revoir
E
cela].
Selon la lecture diagonale, cette case doit servir à porter la valeur
décimale de la dimension : c'est la courbure de cette surface qui
correspond à cette valeur. Pour la dimension fractale "0", cette
valeur décimale était donc seulement unidimensionnelle, pour
la dimension fractale "1", la valeur décimale était le résultat
de la combinaison de 2 dimensions, et pour la dimension fractale "2", cette
valeur décimale est donc la combinaison de 3 dimensions : les 2
dimensions qu'il faut pour faire une surface, plus la valeur de la déformation
de cette surface.
Que l'unité de
mesure de cette dimension soit une surface peut se comprendre de la façon
suivante :
Il s'agit de mesurer la déformation
d'un corps sur lui-même, ce qui implique que tous les points de ce
corps se coordonnent de façon permanente entre eux pour s'échanger
leur place. Pendant toute la déformation, il faut en effet qu'il
n'y ait jamais deux points qui occupent le même emplacement, car
cela laisserait des places vides, des trous aux endroits délaissés,
et cela créerait des surdensités aux endroits suroccupés.
Chaque point suit donc son propre
trajet, ce qui correspond à une dimension 1, et doit jouer en même
temps un rôle dans la dimension de densité du corps pour que
cette densité reste constante. Or, une dimension de densité
est une dimension de contraste de type "0".
Chaque point est donc soumis
à l'influence simultanée de 2 dimensions de types différents
: une dimension de type "1" et une dimension de type "0".
Quand un point est soumis à
la coordination de 2 dimensions similaires, cette coordination peut se
résumer dans une seule dimension de type "1", ainsi qu'on l'a vu
à la ligne précédente, mais quand chaque point
est sous l'influence de deux dimensions de nature différente, elles
ne peuvent se combiner et l'évolution du point doit être décrit
simultanément par ces deux dimensions.
Deux dimensions, cela fait donc
une surface.
C'est à décrire
l'évolution de cette surface que doit servir une dimension fractale
"2".
|
- dans la
2ème case de cette dimension, on trouve la dynamique d'évolution
de cette surface. On a vu qu'il s'agit d'un "attracteur étrange"
autosimilaire à lui-même à toutes les échelles
[revoir E
cela].
La position de cette case dans la lecture diagonale du tableau correspond
à la synchronisation entre toutes les échelles, ce qui est
bien cohérent avec la dynamique d'un attracteur étrange.
- en
3ème case, nous trouvons que cette dimension se manifeste par
des valeurs statistiques et non des valeurs continues. Chaque point obtenu
est l'un des croisements des "0" et "1" qui s'exercent en même temps
pour faire la surface décrite dans la 1ère case. Ces croisements
ne peuvent pas être reliés en continus l'un l'autre, car cela
voudrait dire que ces 2 dimensions 0 et 1 de nature différente ont
trouvé une dimension de coordination commune, ce qui est impossible
ou nous ramènerait à la dimension fractale de la ligne précédente.
Cette case doit porter la valeur du nombre entier de la dimension fractale
: que chaque point soit le croisement de 2 courbes séparées
correspond bien à la valeur "2" de cette dimension.
On a dit que cette dimension sert
à mesurer les phénomènes liés à la force
nucléaire de cohérence de la matière, parce que les
particules de matière sont fondamentalement des corps qui se déforment
sur eux-mêmes [revoirE cela].
- dans la
4ème case, nous avons la façon dont nous apparaît
la dimension. Ce qui nous apparaît est donc un corps qui se déforme
sur lui-même par l'échange de position coordonnée de
tous ses points. Dans la lecture diagonale du tableau, cette case est celle
de la dimension complexe. Nous ne connaissons pas assez la mathématique
des nombres complexes pour interpréter cette case.
La 4ème et dernière ligne correspond aux dimensions fractales
qui ont 3 pour partie entière, et qui sont donc les dimensions usuelles de l'espace-temps.
|
- dans sa
1ère case, nous avons mis l'état "de ce qui sert à
la mesurer" : c'est un volume d'espace. Comme il intègre les 3 dimensions
des lignes précédentes, il doit être muni de 3 courbes
pour correspondre au croisement de 3 dimensions de natures différentes
et impossibles à combiner entre elles. Cette case étant
celle de la dimension d'autosimilarité d'échelle, aussi bien
dans le sens diagonal que dans le sens vertical de lecture du tableau,
ses courbes doivent être autosimilaires. Elles doivent donc être
droites, avoir même origine et même unité de mesure.
- dans
la 2ème case, nous avons la dynamique de ce repère 3
D. Cette dynamique consiste à repositionner en permanence tous les
points à la même place par rapport au point qui sert d'origine.
L'absence de mouvement qui en résulte n'est pas due à l'absence
réelle de mouvement, mais à la combinaison complexe du mouvement
dans les 3 directions de l'espace, de telle sorte qu'en permanence ces
mouvements se neutralisent exactement. La fixité qui en résulte
est donc due à une coordination dans 3 dimensions distinctes, c'est
pourquoi "3" est la valeur entière de la dimension fractale qui
exprime cette case.
- dans
la 3ème case, nous avons la dimension complexe sous laquelle
doit se faire la mesure. L'essence de cette mesure est qu'elle se fait
"d'un point à un autre", c'est-à-dire que l'on mesure la
position de chaque point par rapport à l'origine.
Si l'on observe toute la 3ème
colonne en remontant, on voit que cette mesure se fait en augmentant chaque
fois le nombre des dimensions des "instruments de mesure" :
- dans la dimension 3 donc, la mesure se fait à l'aide de points,
- dans la dimension 2 juste au-dessus, la mesure se fait à l'aide de l'intersection de deux courbes,
- dans la
dimension 1 encore au-dessus on l'a représentée avec
des vecteurs qui occupent toutes les directions de l'espace mais la valeur
de ces vecteurs s'exprime finalement par la surface que forme leurs extrémités,
- et dans
la dimension 0 enfin, c'est tout un volume que l'on doit comparer
à un autre pour mesurer la proportion entre les deux. La proportion entre 2 surfaces ou entre 2 longueurs ne sont que des cas particuliers dans lesquels 1 ou 2 dimensions des volumes à comparer sont nulles.
Si l'on redescend cette 3ème
colonne, l'instrument de mesure se transforme donc de la manière
suivante : des volumes, des surfaces, des trajets, des points.
La même évolution par
gain d'une dimension chaque fois se fait aussi pour les figures que l'on
rencontre dans les autres colonnes.
- dans la
1ère colonne, qui concerne "l'unité de mesure", on
commence avec un point pour la dimension fractale 1, puis on passe à
la courbe, puis à la surface, et enfin au volume.
- dans la
2ème colonne qui concerne la dynamique de l'unité
de mesure, on commence par le point fixe avec la dimension 3, puis on continue
avec la dimension 0 et la dynamique du trajet continu (on sait que le tableau
se poursuit indéfiniment en remettant à sa suite les lignes
précédentes), ensuite vient la dimension 1 et la coordination
de 2 dimensions qui a valeur de surface constante, puis avec la dimension
2 on trouve l'attracteur étrange dont on a vu par l'exemple du robinet
qui goutte, qu'il se construit en groupant des coordonnées par 3.
Au passage, on peut noter que
cela implique qu'un attracteur étrange soit donc une figure qui
a valeur de volume et dont l'unité élémentaire soit
une surface.
- la 4ème
colonne concerne la façon dont la dimension apparaît finalement
sous la forme du phénomène que l'on observe. On y retrouve
aussi une progression de ligne à ligne, mais cette fois cette progression
a un caractère plus abstrait car l'on y trouve l'essence de ce que l'on a désigné par "les dimensions
selon l'univers"
Cette notion des 4 dimensions selon l'univers [2e colonne, avant les 4 colonnes, proprement dites, du tableau] se réfère aux 4 stades successifs par lesquels passe tout phénomène naturel qui se complexifie, tels qu'ils sont décrits de façon résumée au chapitre 1.2 de la l e partie (Présentation de l'hypothèse) de l'essai « En attendant le Boson de Higgs » . L'essence de ces dimensions selon l'univers est qu'elles ne constituent pas seulement la combinaison d'un nombre de plus en plus grand de dimensions : en naissant, chacune opère une véritable mutation de nature qui la différencie radicalement des autres. On va voir que la valeur des dimensions fractales correspond à la valeur des « dimensions selon l'univers » qui « font la même chose », ce qui est d'autant plus remarquable que chaque case du tableau des dimensions fractales est décalée d'une dimension, si on la compare à celle du tableau des dimensions selon l'univers
Dans cette 4ème colonne :
- la dimension fractale 0 mesure une certaine densité de mutation. Par exemple, elle peut mesurer dans quelle proportion un solide se métamorphose en liquide, ce qui correspond à l'ultime étape de la dimension 0 selon l'univers, celle que l'on a définie comme étant la dimension des « points séparés » [chapitre 2-4, à la 4 e étape du cycle de formation de la matière].
- la
dimension fractale 1 correspond à un mouvement qui fait s'écarter
un point dans toutes les directions de l'espace, et qui peut le faire éventuellement errer sans jamais le faire revenir à l'une de ses
anciennes positions. Par exemple, lorsqu'elle a la valeur maximale de 1,999999...
cette dimension mesure la dispersion complète d'un gaz dans l'air
d'une pièce sous l'effet du mouvement brownien de ses molécules
[voir E
cela - on peut aussi se reporter au chapitre 2-5, à la 5 e étape du cycle de formation de la matière].
Cette dimension fractale est équivalente à la dimension 1
selon l'univers, c'est-à-dire à la dimension que l'on a appelée « du classement », lequel classement culmine dans l'organisation en spirale ou en hélice d'hélice qui parvient à réguler la dispersion dans l'espace de façon similaire sur toutes les échelles [chapitre 2-8, à la 8 e étape du cycle de formation de la matière].
- la
dimension fractale 2 correspond à la déformation interne
d'un corps. Elle est équivalente à la dimension 2 selon l'univers
qui organise le mouvement en cycles fermés [chapitres 2-10 et 2-11, aux 10 e et 12 e étapes du cycle de formation de la matière]. La dimension selon l'univers fait donc très exactement la même chose que la dimension fractale qui lui correspond.
- la
dimension fractale 3 correspond à "l'espace-temps traditionnel".
Il nous reste à en voir la 4ème case sous laquelle cette
dimension nous apparaît.
|
- dans la 4ème
case, nous retrouvons l'espace-temps traditionnel.
Nous n'avons pas besoin d'innover,
nous l'illustrons comme la tradition : un point qui se déplace forme
une droite qui se déplace pour former un plan qui se déplace
pour former un volume. Dans le sens diagonal, cette case correspond à
la valeur décimale de cette dimension. Cette valeur décimale
dépend de la vitesse relative avec laquelle ces 3 déplacements
s'effectuent.
On remarque que l'espace-temps obtenu
par construction d'une droite puis d'une surface puis d'un volume, ne changera
pas si l'on se sert d'un autre des 3 axes pour servir de 1ère droite
par laquelle débute la construction : l'ordre des 3 déplacements
qui génèrent le volume est permutable. Les 3 dimensions sont
donc devenues similaires entre elles, et cela à toutes les échelles.
Dans sa signification de "dimension selon l'univers" [voir
E plus
haut à quoi cela correspond],
la dimension 3 correspond aussi à l'interférence autosimilaire
des 3 premières.
Nous trouvons
donc dans la signification de la dimension fractale 3, la réconciliation
enfin obtenue des 3 premières dimensions fractales : elles trouvent
enfin le moyen de se combiner de telle façon qu'on ne peut plus
différencier les 3 axes de l'espace, attribuer l'un ou l'autre spécialement
à la dimension 0 ou à la dimension 1 ou à la dimension
2.
À l'issue de toutes ces réflexions,
la conception traditionnelle de mesure de l'espace par 3 axes orthogonaux
gradués nous apparaît donc comme une méthode parmi
quatre méthodes radicalement différentes l'une de l'autre
pour mesurer les phénomènes, quatre méthodes complémentaires
l'une de l'autre, et toutes contenues les unes dans les autres.
Finalement ce que l'on a découvert,
c'est qu'une
dimension n'est rien d'autre au fond que l'une des 4 façons possibles
de combiner entre elles 4 dimensions, l'une des 4 façons possibles
de faire permuter leurs rôles complémentaires.
L'intérêt
que peut présenter ce tableau serait d'aider à comprendre
comment mesurer de façon "non probabiliste" les dimensions fractales
2.
De façon générale, l'idée serait de penser comment
chaque dimension est la "dérivée" de la dimension juste au
dessus, et sert de "primitive" à la dimension juste en dessous.
L'introduction des dérivées
par Newton et Leibniz a été en effet l'instrument mathématique
qui a permis tous les développements du calcul scientifique depuis
le XVIIème siècle.
Aujourd'hui, on considère
toujours qu'une dérivée est le changement instantané
que subit la direction d'une courbe : elle serait la limite de ce changement
quand la durée de temps tend vers 0. Malgré l'efficacité
de cette conception, il était malcommode de penser qu'un changement
pouvait être véritablement réalisé en un temps
nul : dans un temps nul, un changement ne peut qu'être nul.
Notre hypothèse qui propose
que les dimensions soient fondamentalement des déformations, ne
rencontre pas cette anomalie. Comme nous considérons qu'un trajet
est fondamentalement la coordination de 2 déformations, nous pouvons
très bien arrêter l'une des déformations en la rendant
nulle, afin de mesurer l'autre déformation qui n'a pas alors de
raison spéciale d'être nulle. Dans
notre hypothèse, c'est cette valeur que prend l'une des déformations
d'un trajet lorsque sa déformation associée s'annule, que
nous appelons "dérivée".
La dynamique des dimensions 2 présente
un caractère "volumique" qui provoque son caractère statistique,
car on ne peut pas calculer les côtés d'un parallélépipède
si on n'en connaît que le volume. Peut-être
l'analyse de ce tableau permettra-t-elle à quelqu'un de trouver
comment trouver l'évolution de la surface d'une des faces de ce
parallélépipède, et de connaître ainsi de façon
absolue la longueur des arêtes
?
ÉPILOGUE
D'abord dans l'essai « l'adieu au big-bang », puis dans l'essai « en attendant le Boson de Higgs », est longuement décrite l'hypothèse d'une évolution des ondes d'espace au fil du temps.
Le dernier tableau de ce présent texte sur les dimensions des nombres se boucle sur la notion d'espace-temps.
Peut-on maintenant proposer une façon de penser le temps par rapport à l'espace, afin de ramener la naissance du temps à la synchronisation des ondes d'espace qui marqua, comme on l'a supposé, le début de notre univers ? Certainement.
Selon notre hypothèse, le temps apparaît en effet clairement comme la dimension même d'autosimilarité que se sont trouvées les trois dimensions de l'espace, c'est-à-dire comme la 4ème dimension qui naît toujours pour correspondre à l'interférence de 3 premières dimensions lorsqu'elles ont réussi à se coordonner à toutes les échelles de l'espace à la fois.
Toujours, on l'a donc proposé dans les essais cités plus haut, les ondes d'espace complexifieraient leurs déformations de façon irréversible.
À la conception habituelle qui veut que tout ce qui se passe dans l'espace soit réversible et que le temps, lui, file irrésistiblement, nous opposons donc une hypothèse où l'espace se transforme irrésistiblement et où l'on nomme temps ce changement continuel et toujours similaire à lui-même.
L'espace nous file entre les doigts.
Le temps est la mesure cette glissade.
Texte rédigé en 1993
Mise à jour de détail : 21 février 2010
Il est rappelé qu'une version continue de cette série de textes sur les dimensions des nombres est disponible en version pdf à l'adresse : dimensions-des-nombres.pdf
| I
accueil |
E
Math |
G
haut |
|
O
auteur
|