I
accueil |
E
sommaire
Mathématique |
avant
: E
Ian Stewart fait goutter
son robinet |
suite
: F
pour voir se qui se passe
dans la 4ème dimension |
RAPPEL : une version de l'ensemble du développement, revue et améliorée dans le détail, est disponible en format pdf à l'adresse : Dimensions des nombres
Naissance d'une dimension
On a commencé à parler
de l'interférence entre les trois causes de déformation courbe
qui produisent les gouttes.
L'hypothèse que l'on va faire
sur la cause de l'apparition du chaos, a trait à une caractéristique
particulière que va prendre à un certain moment cette interférence.
Ian Stewart explique dans son livre
"Dieu joue-t-il aux dés ?" [revoir
E ces
références de cet ouvrage]
que quand le chaos apparaît, il y a toujours en même temps
quelque chose qui devient autosimilaire dans le phénomène.
On
fait ici l'hypothèse que c'est la déformation résultante,
celle produite par l'interférence entre les trois déformations
courbes initiales, qui devient alors autosimilaire et provoque aussitôt
l'apparition du chaos.
On explique maintenant pourquoi.
Si les trois causes engendrent entre
elles une déformation combinée autosimilaire, cela veut dire
qu'à chaque échelle où l'on peut considérer
l'eau en train de former une goutte, l'interférence entre les trois
déformations courbes (pression, gravité et tension
capillaire) forme une partie d'interférence en phase avec l'interférence
globale.
Ce que cela change, c'est que si
maintenant on augmente encore un peu la pression qu'exerce la 1ère
déformation, ce supplément va être encaissé
de façon coordonnée à toutes les échelles du
liquide.
Puisque le nombre d'échelles
où un phénomène peut se diviser tend vers l'infini,
cela veut dire que ce supplément de déformation va être
divisé presque à l'infini. Il va être émietté,
saucissonné entre toutes les échelles du liquide. Il perdra
proportionnellement, donc "infiniment", de son pouvoir déformant.
Or, diviser à l'infini,
c'est réduire à zéro.
Ce qui est valable pour la déformation
par la pression, vaudra de la même façon pour les deux autres
causes de déformation : soudainement, chacune des trois prendra
donc une valeur nulle.
Ceci peut se résumer
en disant que le caractère autosimilaire acquis par l'interférence
des trois déformations courbes devient une cause de stabilisation
de la déformation, une cause qui s'oppose à tout surcroît
de déformation en l'éparpillant sur une infinité d'échelles.
L'autosimilarité agit donc comme une
force qui contraint le phénomène de déformation
à se réduire.
Elle "déforme la déformation"
du phénomène.
Elle devient ce qu'on peut bien
appeler une nouvelle cause de déformation,
puisque sans elle le phénomène aurait pris une autre forme.
|
Nous venons de dire qu'une cause
qui fait stopper une déformation mérite d'être appelée
elle- même "déformation". Il n'y a pas de quoi en être
choqué, car c'est strictement similaire au cas d'une force qui s'oppose
par exemple à la progression d'un objet : on pousse l'objet en lui
imprimant une force et son déplacement occasionne un frottement
qui stoppe ce déplacement. Le frottement qui arrête l'objet
reçoit le même nom de "force" que la cause qui pousse l'objet.
Ici, ce qui s'oppose au changement
est appelé "déformation", de la même manière
que la cause opposée qui tend à l'accroître.
L'autosimilarité est
donc une cause de déformation. Mais plus que cela, c'est une
cause de déformation autonome, une cause distincte des trois
premières, car celles-ci tendent à accroître la déformation,
alors que la nouvelle tend à la limiter.
Bien qu'étant le résultat
de leur interférence, elle n'a donc rien à
voir avec "l'addition" de ces trois causes.
Précédemment,
on avait donné un schéma
[revoir E
ce schéma]
indiquant comment le principe d'addition vectorielle des forces pouvait
se trouver parfois mis en défaut par l'allure de l'interférence
de ces forces. C'est probablement maintenant où l'explication de
ce qui arrive au phénomène est tout entière contenue
dans la caractéristique de l'interférence, que cette représentation
vectorielle traditionnelle est la plus handicapante : tout
lui échappe, elle nous aveugle complètement sur ce qui se
passe.
Ce n'est pas la première
fois qu'on est amené à considérer que le caractère
autosimilaire d'un phénomène agit comme une force. Ainsi,
Pierre Gilles de Gennes, dans un article "la matière ultradivisée"
[L'Ordre du Chaos - Bibliothèque Pour La Science - diffusion
Belin - 1989] en avait donné un autre exemple.
Il considérait des grains
de peinture entourés chacun d'une auréole de polymère.
Les chaînes de polymères se mettent d'elles-mêmes en
réseau autosimilaire à toutes les échelles. Et Pierre
Gilles de Gennes conclu que cette autosimilarité des réseaux,
lorsqu'elle cherche à se reproduire également dans l'interférence
entre les auréoles de tous les grains, agit alors comme une force
qui repousse les grains les uns des autres. L'autosimilarité des
réseaux d'auréoles empêche les grains de coalescer,
c'est-à-dire de s'agglomérer entre eux comme ils le feraient
en l'absence des auréoles.
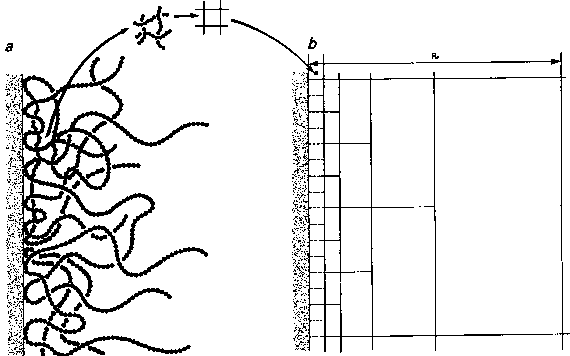 la
structure autosimilaire d'une auréole diffuse de polymère
autour d'un grain,
selon P.G. de Gennes
|
Pour en revenir au robinet qui goutte,
nous avons donc dans l'évolution de l'interférence entre
les trois forces qui causent les déformations, un moment où
cette interférence acquiert une propriété d'autosimilarité
qui la transforme elle-même en force :
-
en force distincte et autonome des trois premières forces,
puisqu'elle n'agit pas de la même manière qu'elles ;
-
en cause nouvelle de déformation
qui agit dans tout le volume et à toutes les échelles de
façon similaire.
Nous avons donc là
exactement toutes les propriétés qu'il faut pour qu'une cause
de déformation soit appelée "dimension" : elle
déforme, pour son propre compte, dans toutes les directions, et
de même façon à toutes les échelles. C'est une
dimension de déformation courbe autosimilaire. Par conséquent,
c'est une "dimension fractale".
Nous avions donc commencé
avec un robinet qui gouttait dans l'espace 3 D (3 dimensions d'espace),
sous l'influence d'un phénomène 3 D (3 dimensions de déformation).
Puis soudain nous nous retrouvons
avec un robinet qui continue à goutter dans l'espace 3 D,
mais qui subit maintenant l'influence d'un phénomène 4
D (4 dimensions de déformation).
La description la plus immédiate
de ce qui se passe alors, est de dire que les dimensions d'espace se trouvent
"débordées" par le nombre des dimensions du phénomène.
Les dimensions d'espace ne peuvent plus contenir en continu toutes les
dimensions du phénomène, car l'autosimilarité
lui donne une dimension en trop pour cela.
Mais rien ne peut empêcher
le phénomène d'avoir plus de dimensions que son réceptacle.
Cela ne gêne pas le phénomène d'avoir plus de dimension
que l'espace où il évolue.
En conséquence, rien ne change
pour le phénomène : il continue d'être parfaitement
déterminé par l'interférence de ses dimensions fractales
de déformation qui sont maintenant 4.
Il n'y a que pour nous que cela
change quelque chose, car dans l'espace 3 D, on ne peut voir se développer
de façon continue que 3 dimensions de déformation à
la fois. Nécessairement, la 4ème
dimension de déformation ne correspond plus à des liens de
proximité dans l'espace, ne correspond plus à une continuité
visible dans l'espace.
Pour nous, c'est donc le chaos apparent.
Visiblement, des parties du phénomène
sont éparpillées sans lien de continuité entre elles,
mais, dans la réalité
des causes qui agissent dans le phénomène, elles sont liées
et continues l'une l'autre dans toutes leurs 4 dimensions.
|
Pour donner un équivalent
de ce que signifie "être relié en réalité mais
pas visiblement", on peut s'imaginer que l'on est un être 1 D (une
droite par exemple), et que l'on cherche à apercevoir un carré
(réalité 2 D) qui nous traverse.
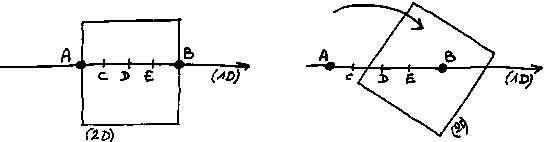
En tant que créature 1
D, tout ce que nous pouvons voir et saisir du carré, ce sont les
points A et B où il nous traverse.
Pour nous, ces 2 points sont parfaitement séparés, discontinus.
Il y a une infinité de points C, D, E, F, etc. qui les séparent
et les empêchent d'être liés. Nous sommes incapables
de concevoir que ces 2 points soient, en réalité, reliés
en continu par une figure carrée, car pour nous, dans notre univers
1 D, un carré cela n'existe pas, cela n'a pas de sens. Tout ce qui
est continu pour nous entre A et B doit forcément passer par C,
D, etc.
Si le carré se met à
bouger, à glisser
par exemple le long de notre droite-univers, nous serons incapables de
saisir un rapport quelconque entre le fait que le carré quitte le
point A, et le fait qu'il quitte en même temps le point B.
Cela sera pour nous deux déplacements
dont les causes nous paraîtront indépendantes. Si, par-dessus
le marché, le carré se met à tourner en même
temps qu'il glisse, le rythme de déplacement de B va varier en conséquence
d'une façon différente de celui de A. Le rapport entre ces
deux rythmes nous paraîtra complètement aléatoire,
en particulier quand le sens de déplacement d'un point changera
au passage d'un des sommets du carré sur la droite.
On dira de ce rapport qu'il
est chaotique, mais il ne l'est pas dans la réalité.
Il ne nous apparaîtra ainsi que parce que la cause qui génère
son évolution (le déplacement d'un carré qui pivote
sur lui-même) a une dimension de trop pour être saisie en continu
dans notre univers 1 D.
Quand
l'autosimilarité transforme un phénomène 3 D + T (le
temps) en phénomène 4 D + T, c'est exactement la même
chose pour nous qui vivons dans un univers 3 D + T. Nous sommes incapables
de voir, de saisir, ce qui relie en continu ce qui se produit dans une
4ème dimension.
À la question parfois posée
: "où se cache l'ordre caché du chaos déterministe
?", nous sommes donc en mesure de proposer cette réponse :
il ne se cache pas ! Il évolue seulement dans une 4ème dimension
à laquelle nous sommes aveugles, car nous ne pouvons voir en continu
dans l'espace que 3 dimensions à la fois.
Mais prenons bien garde à
considérer qu'il n'évolue pas dans une 4ème dimension
d'espace qui n'existe pas, mais dans une 4ème dimension de déformation.
Ce qui pour nous
fait chaos, c'est que l'espace n'a que 3 dimensions, ce qui est insuffisant
pour rendre compte de la continuité simultanée de 4 dimensions
de déformation.
| I
accueil |
E
Math |
G
haut |
suite
: F
pour voir se qui se passe dans la 4ème dimension |
O
auteur
|