
(à poursuivre à l'infini)
| I
accueil |
E
sommaire Mathématique |
avant
: E
comment voyager d'un nombre à l'autre |
suite
: F
dimensions fractales et dimensions d'espace |
| accès direct à tous les autres textes de la section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
Après ce grand détour
qui nous a appris à penser autrement les valeurs décimales,
nous revenons maintenant aux déformations courbes.
Nous les avions laissées
[revoir E
ce moment] en
disant qu'en chaque point nous voulions représenter l'ensemble des
sollicitations qui tendent à déplacer ce point dans l'espace.
Et nous avions alors admis que ces sollicitations devaient être représentées
par un nombre infini de vecteurs, ayant chacun une intensité spécifique,
et chacun étant orienté dans une direction spécifique
de l'espace.
Pour représenter par un ensemble
de vecteurs les sollicitations variées qui forcent un corps à
bouger, nous devons
donc avoir à notre disposition 3 types distincts de données
:
1/
d'abord nous devons indiquer que, dans ce cas, ce qui arrive au corps matériel
est une déformation de sa position, c'est-à-dire un mouvement
dans l'espace. Il aurait pu s'agir d'une autre sorte de déformation
: cela aurait pu être une déformation tendant à le
percer, ou à l'étirer, ou à faire gonfler son volume,
ou à le compresser.
2/
ensuite, nous devons indiquer l'intensité de cette déformation.
3/
enfin, nous devons indiquer comment varie cette intensité selon
les différentes directions de l'espace.
Or, il se trouve que notre analyse
de la génération des nombres entiers et décimaux nous
a montré qu'un
nombre fractionnaire portait nécessairement 3 types différents
d'informations :
1/
la première concerne le nombre entier auquel il est lié.
2/
la seconde concerne l'ordre séquentiel des déformations successives.
3/
la dernière, concerne la valeur de cette déformation pour
chacune des séquences décimales.
|
Cela nous suggère un moyen simple pour mesurer une dimension de déformation courbe à laquelle un point est soumis : il suffit d'utiliser un nombre irrationnel. Sa partie entière dira le type de déformation dont il s'agit, et chaque chiffre de la suite décimale portera la valeur d'intensité pour une des directions de l'espace. Ces directions sont en nombre infini mais le nombre des décimales d'un irrationnel l'est également. Nous viennent alors à l'esprit
les dimensions fractales de Mandelbrot.
|
Envisageons d'abord le chiffre entier qu'elles
comportent avant la virgule.
- 0 -
nous avions commencé à présenter les dimensions de
déformation en donnant des exemples de déformations
de contrastes.
Ainsi, nous avions évoqué la "poussière de Cantor"
: un segment dont on a enlevé le 1/3 central, puis enlevé
le 1/3 central des 2 segments restants, puis etc., à l'infini.
[revoir E
cette figure]
Il se trouve que la dimension fractale
d'une telle poussière de Cantor où la déformation
n'implique aucun déplacement, est Log 3/ Log 2, c'est-à-dire
environ 0,63.
Sa partie
entière est donc 0.
- 1 -
Ainsi que nous le verrons dans les exemples prochains [images ci-dessous],
les
valeurs fractales des trajets
que Mandelbrot indique dans son ouvrage "les objets fractals" [Flammarion
- 3ème édition - 1989], se trouvent toutes comprises
entre 1 et 2.
C'est-à-dire que leur
partie entière est toujours 1.
- 2 -
Enfin, on constate que la valeur fractale d'une "courbe de Peano" est 2
[Voir F
cette figure dans le texte suivant].
Or le principe de cette courbe, est de déformer le découpage
d'une surface sur elle- même de telle sorte que change régulièrement
la distribution de ses parties blanches et de ses parties colorées,
sans cependant que leur proportion réciproque ne soit modifiée.
Pour obtenir ce résultat, à chaque stade de son tracé
la courbe réalise une division plus tortueuse entre les deux parties
de la surface.
Alors on se dit que peut-être
la
valeur entière 2 dans une dimension fractale a à voir avec
la déformation d'un corps sur lui-même.
Quant à la valeur décimale
des dimensions fractales,
nous savons que la plupart du temps elle correspond à un nombre
irrationnel, résultant de la division de deux logarithmes. Ainsi,
elle contient bien une suite infinie et ordonnée d'informations.
Il reste à envisager la représentation
graphique de ces dimensions.
Mandelbrot donne l'exemple [ouvrage
cité ci-dessus d'où son extraits les graphiques] de la
dimension fractale Log 4/Log 3, c'est-à- dire environ 1,2618,
pour la courbe en "flocon de neige" de Von Kock. Cette courbe ne
peut pas être réellement dessinée, car elle correspond
à un processus infini. On prend un triangle équilatéral.
Sur chaque côté du triangle, on construit un triangle équilatéral
porté par son 1/3 central. Sur chaque côté des derniers
triangles réalisés on construit . . . etc. à l'infini.
 |
génération
du "flocon de neige" de Von Kock
(à poursuivre à l'infini) |
 |
le "flocon
de neige" de Von Kock
Dimension = Log 34 ~ 1,2318 |
| Autre exemple : pour une valeur de dimension fractale Log 5/Log 4, c'est-à-dire environ 1,16, on obtient ce genre de courbe que l'on doit aussi poursuivre à l'infini, et dont ne sont représentées ici que les premières étapes. | 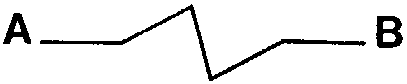 |
 |
Dimension = Log 45 ~ 1,16 |
Comment
retrouver une valeur fixe à la dimension fractale d'un trajet
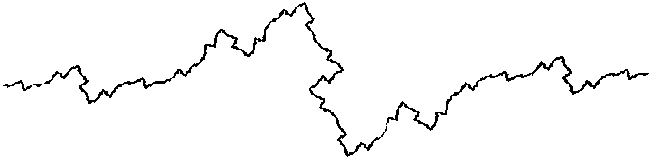
Si maintenant on regarde la courbe
AB du dessin précédent, non plus comme une figure dessinée,
mais comme le trajet d'un mobile qui va de A jusqu'à B, on se dit
que ce type de trajet évoque assez bien ce qui se passe quand un
corps est entraîné vers un autre par une déformation
courbe : le graphique montre qu'il part de A, arrive à B, et que
pour réaliser ce trajet il ne subit pas une attraction uniquement
dirigée vers B, mais qu'il est attiré constamment et simultanément
dans d'autres directions.
En somme, s'il finit par arriver
très exactement sur B et pas à côté, ce n'est
que parce que les attractions selon les différentes directions de
l'espace sont bien combinées entre elles, et qu'elles le sont à
toutes les échelles du trajet.
Il y a cependant une objection majeure
que fait Mandelbrot lui-même, à l'utilisation des courbes
fractales comme représentation valide d'un trajet suivi par un mobile.
Cette objection a trait à la longueur du trajet.
En effet, si on calcule la longueur
d'une courbe fractale, on s'aperçoit qu'elle est infinie. Pour la
dessiner, chaque fois que l'on descend d'un cran dans l'échelle
de détail de son parcours, on transforme un segment droit en une
série de segments qui ondulent sur ce 1er segment. Comme la droite
est le plus court chemin entre deux points, chaque étape dans le
"raffinement du détail" a donc pour effet de rallonger la courbe.
Certaines suites infinies convergent vers une somme finie, mais ici ce
n'est pas le cas car le facteur de rallongement du parcours est constant
et ne diminue pas avec l'échelle de détail.
Si la courbe est de longueur infinie,
il ne semble donc pas possible de l'utiliser pour mesurer le trajet parfaitement
fini réalisé par un mobile.
Pour éviter d'obtenir ce
résultat de longueur infinie, on peut décider de ne pas dessiner
la courbe dans tous ses infinis détails et s'arrêter à
un moment donné dans la cascade de sa génération.
Mais alors, selon le degré de détail que l'on prend en compte,
c'est-à-dire selon l'échelle de détails jusqu'à
laquelle on descend, la longueur du trajet obtenu est chaque fois différente.
|
Le trajet fractal serait donc soit de longueur infinie, soit de longueur finie mais variable avec l'échelle de sa mesure ? Une courbe fractale semble ainsi bien mal partie pour servir à représenter le trajet d'un mobile entraîné par une déformation courbe. Cette fois encore, l'analyse que l'on a fait plus haut des nombres décimaux va nous servir à comprendre où réside l'anomalie. |
Concernant cet aspect des dimensions
fractales, nous divergeons donc de la présentation qu'en a fait
Mandelbrot. À
la question : "quelle est la longueur de la côte de la Bretagne ?",
Mandelbrot répond : elle est de longueur infinie
car nous pouvons toujours la suivre sur une échelle plus petite.
Le trajet peut être fait en voiture, ou fait à pied pour en
suivre mieux les méandres, ou au pas d'une souris, ou peut contourner
tous ses grains de sable, ou peut contourner tous les atomes qui en marquent
la limite : à chaque cran de précision la longueur du trajet
se rapprochera de l'infini. À
la même question, nous répondons ici : la côte bretonne
a toujours une longueur finie, mais elle a un nombre infini de longueurs,
chacune correspondant
à l'échelle de mesure que l'on choisit, parmi le nombre infini
des échelles de mesure possibles.
|
Dans un système de mesure par coordonnées, un trajet ne possède qu'une seule longueur. Dans un système de mesure par dimensions de déformation, un trajet possède un nombre infini de longueurs qui sont toutes résumées par un seul nombre. Par conséquent, une dimension fractale contient infiniment plus d'informations qu'une dimension de coordonnées, et demande seulement qu'on lui dise lequel de ces trajets l'on veut. Quand on a répondu à sa demande, elle nous en fournit la longueur. |
| I
accueil |
E
Math |
G
haut |
suite : F dimensions fractales et dimensions d'espace |
|