

| I
accueil |
E
sommaire Mathématique |
avant
: E
les dimensions de Mandelbrot à la rescousse |
suite
: F
la continuité des déformations dans l'espace |
| accès direct à tous les autres textes de la section ----> | 00 | 01 | 02 | 03 | 10 | 11 | 12 | 20 | 21 | 30 | 31 | 32 | 33 | 34 |
Dimensions fractales et dimensions d'espace
| Nous en arrivons maintenant au point
crucial, où nous devons penser les dimensions fractales de la façon
la plus neuve.
Dans l'espace des coordonnées, la dimension 1 correspond aux courbes linéaires, 2 aux surfaces, et 3 aux volumes. Habituellement, en partant du même principe, les dimensions fractales sont considérées comme des dimensions d'espace tronquées, "partielles" : |
| Penser de cette manière, c'est penser avec les vieux réflexes. |
| Une dimension fractale comporte
deux parties : un nombre entier, puis, après une virgule, un nombre
décimal.
Nous avons déjà proposé une signification pour chacune de ces deux parties, nous allons maintenant y revenir de façon plus précise et plus complète, en commençant par le nombre entier. |
"0"
: Nous avons donné précédemment l'exemple
[revoir E
cet exemple]
d'une valeur de contraste mesurée à l'aide de taches sur
une feuille. Il s'agissait alors d'un espace 2 D. À la place de
taches 2 D, nous aurions pu tout aussi bien prendre des bulles noires 3
D tachant un volume blanc lui aussi 3 D. La valeur de contraste, mesurant
par exemple la proportion entre le volume des bulles et le volume de l'espace
total, aurait toujours été inférieur à 1.
Une valeur fractale inférieure
à 1, dont le 1er chiffre est pour cela 0, n'a par conséquent
rien à voir avec une quelconque incapacité à remplir
une courbe 1D.
Le chiffre 0 indique seulement que
le phénomène n'implique par lui- même
le déplacement d'aucun point, qu'il se passe complètement
du déplacement de points pour se manifester. Par contre, il implique
l'apparition ou la disparition d'un nombre infini de points.
De ce
fait, les dimensions possédant cette valeur entière 0 sont
spécialement adaptées à mesurer des mutations :
ce qui était blanc devient coloré, ce qui était jeune
devient vieux, ce qui était inerte devient vivant, ce qui était
sain devient malade, etc.
Il n'y a aucun déplacement
qui puisse relater la transformation d'une personne jeune en une personne
vieille, car avant de devenir vieille, une vieille personne n'est nulle
part parmi les vieilles personnes. Puis un jour, il ou elle apparaît
soudainement parmi les vieux avec cette propriété, semblant
venir de nulle part. Puis un jour il ou elle meurt, disparaissant de parmi
les vieux en même temps que cette propriété.
"1"
: Lorsque nous avons reproduit des exemples de courbes fractales
(par exemple la courbe en flocon de neige de Van Kock [revoir
E cette
courbe]), nous avons vu que
lorsqu'une déformation implique un déplacement dans l'espace,
la valeur entière de la dimension fractale est alors 1.
Ce type
de dimension à partie entière 1 est uniquement consacré
à décrire le mouvement d'un corps.
Il n'est pas adapté pour
décrire ou prévoir la mutation éventuelle de ses propriétés
pendant ce mouvement, ce qui est du ressort des dimensions 0 que nous venons
de voir.
Il n'est pas adapté non plus
pour décrire la déformation qu'il peut subir pendant le mouvement,
ce qui est du ressort de la dimension 2 que nous abordons maintenant.
"2"
: Nous avons déjà suggéré que la valeur
entière 2 de la courbe de Peano [voir ci-après
sa représentation] avait à voir avec la déformation
d'une surface sur elle-même. Nous suggérons maintenant de
façon plus générale, que la valeur entière
2 pour une dimension aurait à voir avec la déformation d'un
corps sur lui-même. Par cela il faut entendre
le déplacement interne coordonné de tous ses points qui s'échangent
les uns les autres, mais sans déplacement global du corps lui-même.
Dans la section "science"
[voir E
ce développement],
nous supposons qu'une particule de matière est le résultat
d'un mouvement excessivement complexe mais qui fonctionne en circuit fermé,
ce qui est très exactement un cas de déformation interne.
Tout
ce qui met en jeu la stabilité des particules de matière
et leur cohérence interne, est donc spécialement concerné
par ce type de dimension.
Laurent Nottale qui a cherché
a combiner la mécanique quantique des particules élémentaires
avec le calcul fractal, aboutit à la même conclusion.
On cite un extrait d'un de ses articles
["L'espace-temps fractal" - Pour la Science - septembre 1995] :
'La dimension deux est,
précisément, celle des trajectoires fractales calculées
à partir des relations d'incertitude d'Heisenberg'
| En résumé, notre
hypothèse est donc que si la dimension fractale est de la forme
0,x c'est qu'il s'agit d'une valeur de contraste, si elle est de la forme
1,x c'est qu'il s'agit de la valeur d'un trajet, et si elle est de la forme
2,x c'est qu'il s'agit de la valeur d'une déformation interne.
Comme nous l'avons fait pour la valeur 0, nous soulignons que les valeurs 1 et 2 n'auraient rien à voir avec le nombre des dimensions de l'espace où se déroule le phénomène : - ainsi, un trajet (dimension fractale 1,x) peut tout aussi bien resté attaché à une courbe, qu'évoluer sur une surface, ou se répandre dans l'espace entier ; - et la déformation d'un corps sur lui-même (dimension fractale 2,x) peut tout aussi bien concerner un corps filiforme, qu'une surface ou un volume. |
| Si la déformation est confinée à ne suivre qu'une ligne ou à ne rester que sur une surface, la valeur décimale sera telle qu'elle fournira une valeur nulle pour toutes les directions alors interdites. |
| Par exemple, une dimension de valeur
2,1 ne doit pas être considérée comme une dimension
plus intense qu'une dimension de valeur 1,1.
Ce point est fondamental lorsqu'il s'agit de comparer les dimensions fractales les unes avec les autres : par exemple, une dimension 1,9999. . . etc., ne serait pas une dimension très proche de la dimension 2. Tout au contraire, elles sont plutôt à considérer comme très éloignées l'une de l'autre : l'une est un trajet extrêmement contourné susceptible de se dérouler même dans un espace 3 D, tandis que l'autre peut ne concerner que la déformation sur elle-même d'une surface, ou encore la déformation sur elle-même d'une courbe linéaire 1 D. [voir l'exemple donné ci-après] |
 |
==> |  |
==> |  |
etc |
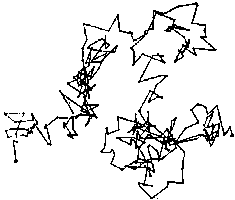 un
échantillon de mouvement brownien : un
échantillon de mouvement brownien :
sa dimension fractale est 2 mais aurait la signification 1,99999999 à l'infini |
| Pour finir, si les dimensions fractales
sont plus générales que les dimensions d'espace, cela implique
que des coordonnées dans l'espace ne doivent être alors que
des dimensions fractales à valeurs spéciales.
Calculons leur valeur : Sur les axes de référence de l'espace euclidien, les coordonnées suivent un trajet droit. En tant que trajet, elles méritent donc la dimension fractale entière 1. Et comme ce trajet reste bien droit et ne subit aucune déformation dans aucune direction, elles méritent la valeur décimale 0. En résumé, les dimensions fractales ne sont pas des dimensions d'espace, spéciales et tronquées, et tout au contraire ce sont les dimensions d'espace qui ne sont que des cas spéciaux et limités de dimensions fractales possédant la valeur très particulière : 1,0. |
| I
accueil |
E
Math |
G
haut |
suite : F la continuité des dimensions dans l'espace |
|