I
accueil |
E
sommaire Mathématique |
avant
: E
reprenons à partir
de zéro |
suite
: F
les dimensions de Mandelbrot
à la rescousse |
RAPPEL : une version de l'ensemble du développement, revue et améliorée dans le détail, est disponible en format pdf à l'adresse : Dimensions des nombres
Comment voyager d'un nombre à l'autre ?
On a pris garde de montrer que la
génération des nombres entiers et décimaux n'avait
rien à voir avec un trajet. Les entiers sont générés
tous d'un seul coup, par la désignation du vide. Et les décimaux
sont générés individuellement, par des séquences
ordonnées de déformations graduées.
On peut cependant avoir besoin de
traduire par des nombres les déplacements que font les particules
ou les objets dans l'espace. Il nous serait donc utile de trouver une équivalence
entre un nombre et un trajet, sans que cette mise en trajet ne fasse perdre
aux nombres leurs propriétés.
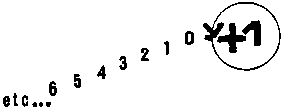 Dans
cette optique, on peut dire que le
trajet qui trahit le moins le mode de génération des nombres
entiers est un trajet circulaire qui part de 0 et qui fait une boucle qui
signifie "+1" en le faisant revenir en même temps à 0.
Dans
cette optique, on peut dire que le
trajet qui trahit le moins le mode de génération des nombres
entiers est un trajet circulaire qui part de 0 et qui fait une boucle qui
signifie "+1" en le faisant revenir en même temps à 0.
Le départ à 0 et l'arrivée
à +1 sont confondus, et tous les nombres entiers sont également
confondus à ce 0/1.
Produire les nombres entiers, c'est
comme tourner sur une boucle sans fin et rencontrer tous les nombres
entiers les uns après les autres, au point de départ et de
retour perpétuel confondus de cette boucle.
Apparemment, la seule perte que
subissent les nombres entiers par cette mise en trajet correspond à
la durée du trajet. Il faudrait pouvoir dire que la durée
de ce trajet est nulle, bien qu'il y ait un écart de temps non nul
entre chaque nombre pour les différencier.
1/
un premier constat doit être fait tout de suite : quand on part de
0 vers 1, 2, etc. jusqu'à l'infini, on ne s'éloigne pas de
0. Ce qui revient à dire qu'on ne s'approche pas d'un point infiniment
éloigné de 0 : on piétine sur place. Le seul rapport
à l'infini que cela peut avoir, c'est que l'on peut y piétiner
indéfiniment, mais toujours sans avancer du moindre pas.
2/
un deuxième constat est à faire : lors de ce piétinement,
on ne peut espérer rencontrer à quelque moment que ce soit
un nombre qui ressemble de près ou de loin à un nombre fractionnaire
ou irrationnel. Car la boucle qui va de 0 à 0 n'a pas "d'arrêt
entre stations". En désignant l'ensemble vide, on a vu que l'on
désignait du même coup 0, 1, 2, 3, etc. Mais on n'a rien pu
désigner en faisant cela qui soit un intermédiaire possible
entre 0, 1, 2, 3, etc. Le trajet qui représente ce processus de
création des nombres entiers ne peut donc s'arrêter quelque
part dans sa boucle entre deux entiers sans dénaturer le processus
qu'il veut équivaloir.
Donc, se déplacer d'un nombre
décimal à l'autre, cela devra n'avoir rien à voir
avec se déplacer d'un entier vers un autre. Il va falloir dessiner
d'autres trajets.
Si l'on tient à démarrer
le trajet vers les décimales à partir du nombre entier qu'elles
suivent après la virgule, on ne peut que constater que tous les
trajets vers les décimales doivent commencer au même point
0, puisque tous les entiers y sont rassemblés.
Si l'on veut maintenant
dessiner à partir de 0 une trajectoire qui conserve toutes les informations
contenues dans un nombre décimal, on peut le faire en dessinant
un réseau hiérarchique de bifurcations tel que celui-ci :
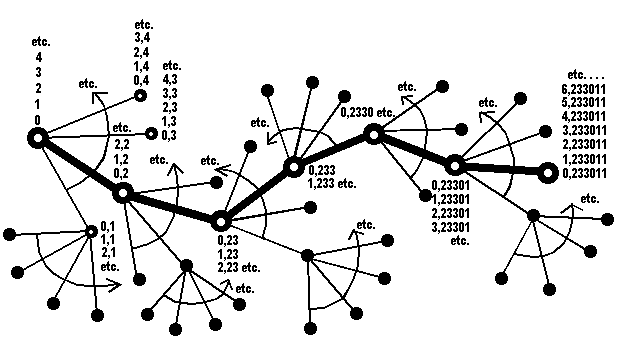 pavage arborescent d'un plan,
par des trajets de nombres décimaux
pavage arborescent d'un plan,
par des trajets de nombres décimaux
À chaque carrefour on
fait partir 10 chemins, et au bout de chacun de ces chemins, on fait un
nouveau carrefour qui s'éclate en 10 chemins, etc. Ainsi, chaque
décimale correspond à un rang de la série des carrefours
rencontrés à partir de 0 (1er, 2ème, 3ème,
etc.), et l'intensité de la déformation indiquée par
chaque valeur décimale correspond à l'un des 10 chemins possibles à partir de ce carrefour.
On peut déclarer par exemple, si l'on va de 0 vers l'infini décimal,
que le chemin le plus à droite qui part de chaque carrefour correspondra
à une déformation nulle, le plus à gauche à
une déformation 9, et chaque chemin intermédiaire à
une déformation intermédiaire entre 0 et 9.
On pourra alors désigner
un nombre décimal par un carrefour d'arrivée, qui sera le
dernier où la déformation ne sera pas nulle.
Comme la structure des trajets est arborescente, il n'existe qu'un seul
chemin qui pourra être pris pour aller de 0/1 à ce carrefour.
La désignation de ce carrefour
suffira donc pour désigner tous les embranchements successifs qui
y mènent, leur ordre et leur intensité correspondante, donc
à désigner l'ensemble de la valeur décimale.
Ce schéma de circulation
offre donc la possibilité de générer des trajets qui
vont atteindre tous les nombres décimaux tout en respectant les
caractéristiques qui les différencient les uns des autres.
Sa lecture amène à faire plusieurs constats :
1/
d'abord, on trouve le cumul à chaque carrefour d'une infinité
de nombres, tous ceux générés de la même façon
après la virgule mais partant chaque fois après un nombre
entier différent. On y retrouve donc la propriété
de piétinement qui est celle du trajet qui relie les uns aux autres
les nombres entiers. On passe de 1,2102 à 2,2102 par exemple, en
reproduisant au carrefour x,2102 la boucle circulaire et sans interruption
qui va de 1 à 2.
2/
ensuite, on constate que l'on ne peut pas utiliser un carrefour décimal
pour désigner un nombre complet avec sa partie entière et
sa partie décimale. C'est la réciproque de ce qu'on avait
vu avec le trajet des entiers : on n'y trouvait aucune décimale.
Sur le trajet des décimales, on ne trouve cette fois aucun entier.
3/
enfin, contrairement aux trajets des entiers, on trouve bien cette fois
chez les décimales matière à voyager jusqu'à
l'infini. On peut prendre n'importe quel chemin à partir des entiers
et s'enfoncer indéfiniment dans la "profondeur infinie" des nombres
décimaux. Tout voyage réellement infini parcourt un nombre
irrationnel, ou parcourt un nombre fractionnaire dont les décimales
alternent dans une périodicité qui se poursuit indéfiniment.
Si maintenant on cherche à
mesurer les déplacements que l'on fait en suivant les nombres décimaux,
et à rapporter cette mesure aux déplacements que l'on fait
en suivant les nombres entiers, on est obligé de conclure que lorsqu'on
avance vers l'infini, c'est-à-dire vers l'extrémité
des trajets décimaux, on n'avance pas d'un pouce dans la direction
des nombres entiers.
En d'autres termes, 3,99999 par
exemple, ne peut absolument pas être considéré comme
plus proche de 4 que ne l'est 3,2. Au contraire même, si l'on ne
parle que de distance à parcourir, on passe plus vite de 3,2 à
4 (1 seule étape dans le parcours décimal) que de 3,99999
à 4 (5 étapes).
Cette anomalie vaut aussi pour les
nombres décimaux entre eux. En terme de distance, 3,2 est plus près
de 3,9 que de 3,2000001.
Mais faut-il faire ce genre de constatations
et partir dans les calculs en se donnant pour acquis par exemple, que 3,2
serait plus près de 4 que ne l'est 3,99999 ?
Ce serait se replonger dans le même
type de situation aberrante que celle où Cantor nous
avait plongé avec les infinis.
La seule chose raisonnable que l'on
puisse faire, est d'admettre ce qui est maintenant évident, à
savoir :
1/
que les nombres entiers sont dans une dimension incommensurable avec celle
des nombres décimaux,
2/
et qu'à l'intérieur même des nombres décimaux,
la position dans la queue décimale, est une grandeur incommensurable
avec la valeur du chiffre indiqué à cette position.
C'est une situation qui n'est pas
nouvelle en mathématique. Le nombre "racine carrée de -1"
par exemple, n'est ni positif (son carré serait + 1), ni négatif
(son carré serait alors aussi + 1).
Les mathématiciens ont appris
à traiter ce genre de nombre que l'on ne peut pas ranger sur une
même ligne que les nombres réels positifs ou négatifs,
et les ont appelés "nombres imaginaires" ou encore "nombres complexes".
Ce qu'il faut désormais admettre,
c'est que les nombres décimaux ne peuvent pas non plus se ranger
sur une même ligne que les nombres entiers, qu'ils ont avec les nombres
entiers le même type de rapport que celui qui existe entre les nombres
dits imaginaires et les nombres dits réels.
Dans le cas des nombres imaginaires
et des nombres réels, on dit qu'ils sont "dans des dimensions différentes",
et que les mettre en rapport ne revient pas à les aligner sur une
droite, mais à former un plan que l'on nomme "le plan complexe".
Nous devons
maintenant dire, mais de façon "encore plus complexe", que toute
combinaison d'un nombre entier avec ses décimales revient à
définir les coordonnées d'un point dans "un volume complexe"
: il faut d'abord définir les valeurs décimales dans le plan
des nombres décimaux, puis, quand le bon carrefour est trouvé
"en profondeur et en largeur", il faut donner "l'altitude" qui correspond
au nombre entier que l'on veut associer à cette décimale.
Bref, il faut s'apprêter, pour
multiplier 2 avec 0,1, à devoir prendre encore plus de précautions
que lorsqu'on cherche à calculer la multiplication de 2 avec "racine
carrée de -1". |
En fait, les nombres réels sont aujourd'hui considérés
comme formant partie des nombres complexes, seulement différents
des autres nombres complexes par la simplicité particulière
avec laquelle on peut les manipuler.
De la même façon, nous devons maintenant considérer
que les nombres décimaux de base 10 ne sont qu'une partie spéciale
de l'ensemble des nombres décimaux : une partie spécialement
pratique puisque nous pouvons sans gêne ajouter les décimales
de différents nombres comme s'il s'agissait de nombres entiers, et
puisque nous pouvons multiplier un nombre fractionnaire avec un multiple
de 10 pour transformer sans plus de procès un nombre décimal
en un nombre entier.
Malheureusement, la nature n'est
pas au courant de cette simplicité, et elle laisse
ses phénomènes se développer de telle sorte que, si
nous voulons les traduire en termes mathématiques, nous devons utiliser
les nombres décimaux dans leurs aspects les plus complexes.
C'est cela que nous allons maintenant considérer.
| I
accueil |
E
Math |
G
haut |
suite
: F
les dimensions de Mandelbrot à la rescousse |
O
auteur
|
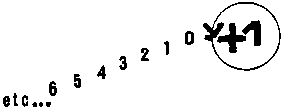 Dans
cette optique, on peut dire que le
trajet qui trahit le moins le mode de génération des nombres
entiers est un trajet circulaire qui part de 0 et qui fait une boucle qui
signifie "+1" en le faisant revenir en même temps à 0.
Dans
cette optique, on peut dire que le
trajet qui trahit le moins le mode de génération des nombres
entiers est un trajet circulaire qui part de 0 et qui fait une boucle qui
signifie "+1" en le faisant revenir en même temps à 0.
