"En théorie", une dimension de contraste peut être auto-similaire
 
 

L'exemple de la feuille tachée présente une faiblesse : on ne mesure pas toujours la même dimension de contraste, même si on mesure toujours la même surface, et même si la proportion des taches y est partout identique. 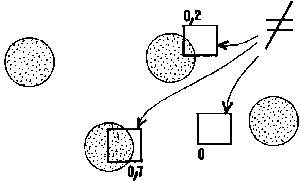   En effet, le résultat va dépendre de la portion de surface sur laquelle on effectue la mesure. Calcule-t-on sur toute la surface ou seulement sur un bout ? Si l'on ne prend qu'une portion et que l'on tombe dans l'intervalle entre deux taches, on trouvera un contraste 0. Alors que si l'on tombe "à cheval" sur une tache, on trouvera un contraste variant aléatoirement entre 0 et 1: cela sera peut-être 0,3 dans une mesure et 0,7 dans une autre.  Si le contraste est homogène sur la feuille, c'est-à-dire si les taches sont également réparties, cela ne change rien. Plus on prend une grande surface, et plus on trouve un résultat constant, mais plus on prend une petite surface, et plus le résultat varie de façon importante et aléatoire.    Il n'existe aucun "truc" pour corriger le résultat en fonction de l'échelle de mesure, et obtenir ainsi toujours le même résultat.

 

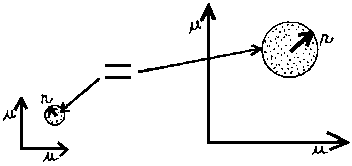Il n'en va pas de même avec les dimensions de coordonnées : on peut regarder les choses de loin ou de près, elles mesurent toujours la même dimension. Il suffit d'adapter l'échelle de mesure à l'échelle de lecture.

 
Pour qu'il en soit de même avec les dimensions de déformation, il faut qu'elles possèdent une caractéristique particulière : il faut qu'elles soient auto-similaires, c'est-à-dire similaires à elles-mêmes à toutes les échelles.
Pour reprendre l'exemple des taches, il faudrait que la taille et l'organisation des taches soient coordonnées de telle sorte que les taches qui semblent continues vues de loin, apparaissent quand on les regarde de plus près constituées de taches plus petites, qui elles-mêmes lorsqu'on se rapproche encore plus, apparaissent constituées de taches encore plus petites, etc... depuis l'infiniment grand jusqu'à l'infiniment petit. Bien entendu, à chaque "niveau de tache", la proportion de blanc et de noir, doit être la même pour que la mesure de la "déformation de la blancheur" soit constante.

Pratiquement ce n'est pas possible, car on ne peut diviser une tache à l'infini, mais théoriquement, c'est possible. Et d'ailleurs cela existe.
     - une "poussière de Cantor" répond à cette définition : c'est une ligne dont on enlève le 1/3 central, et sur chaque 1/3 restant on enlève le 1/3 central, et cela à l'infini.
     - un "tapis de Sierpinski" également : c'est un carré dont on a enlevé le carré central, puis sur chacun des carrés en lesquels on peut décomposer ce qui reste, on enlève le carré central, etc.
     - une "éponge de Menger" est la même chose qu'un tapis de Sierpinski, mais avec des cubes au lieu de carrés.

 

une "poussière de Cantor"

 

une "éponge de Menger"

[les dessins sont repris de l'ouvrage de B. Mandelbrot : les objets fractals - Editions Flammarion]
 
 
 

On a donc un peu avancé dans le définition d'une dimension de déformation.         - d'abord, on a vu comment une déformation pouvait avoir une valeur, indépendamment de toute notion de coordonnées.       - puis, on a trouvé une différence essentielle entre dimensions de déformation et dimensions de coordonnées : les premières oscillent entre 0 et 1, les secondes vont de - l'infini à + l'infini.       - enfin, on a vu qu'une dimension de déformation n'avait pas toujours le caractère autosimilaire à toutes les échelles d'un système de coordonnées, mais qu'elle pouvait obtenir cette particularité dans certains cas.

Après cette première approche, nous sommes préparés pour envisager une deuxième sorte de dimensions de déformation, celle qui correspond à la réalisation de trajets.